Kitten Mixer - A Fun Application of Variational Autoencoders

Have you ever dreamed of combining two adorable kittens into one? Now you can make it come true with the Kitten Mixer app! This project uses variational autoencoders to create unique combinations of cat faces, allowing you to explore how different visual features of these little felines blend together.

In this post, I will briefly explain how the project was carried out from a data science perspective. We begin with an introduction to variational autoencoders. Then, we explore the cat face dataset to understand its features and how these properties impact image generation. Finally, we developed the VAE model, testing different architectures and hyperparameters to achieve the best performance in terms of reconstruction and interpolation quality.

Explore Kitten Mixer and create your own cat combinations! Visit the app now and if you like it, don’t forget to give it a star 🌟 on GitHub to support it.

Introduction to VAEs

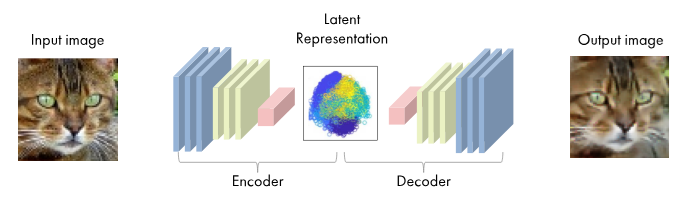
A Variational Autoencoder (VAE) is a neural network model whose ultimate goal is to learn a compressed representation of the original data, called the latent space. Unlike a traditional autoencoder, which only compresses and reconstructs the data, the VAE learns to model the underlying distribution of the data, enabling it to not only reconstruct existing images, but also generate new, realistic images from combinations or interpolations in the latent space.

The latent space is a lower-dimensional representation where the essential features of the images are captured, such as the general shape of the cat, colors, or fur patterns. Once the latent space representations of two cat images are obtained, it is possible to perform interpolations between them, generating intermediate images that show a smooth and continuous visual transition between both. This allows us to explore how different features of two cats would blend in artificially generated images.

Data Exploration

For this project, we used the dataset Cats Faces 64x64 (for generative models). This dataset contains cat face images in \(64 \times 64\) resolution and RGB format, making it ideal for image generation and synthesis tasks, as it reduces computational complexity without sacrificing relevant details.

The dataset includes a total of 15,747 images, all labeled under a single class, “cats”. Although it lacks detailed documentation, the quality and uniformity of the images allow us to focus exclusively on cat face generation, eliminating the variability of multiple domains present in other more complex datasets.

The dataset is highly suitable for image generation tasks, as it presents consistent, high-quality features. The images are properly cropped with minimal background, ensuring that the cat’s face occupies most of each photo. This reduces the complexity associated with variations in the environment or background elements.

Additionally, there is homogeneity in the poses, as most faces are oriented frontally and maintain a similar position across all samples. This uniformity helps the generative model focus its learning on the specific features of cat faces, increasing the likelihood of obtaining coherent and detailed results when synthesizing new images.

Model Development

We tested different VAE model architectures and primarily experimented with various hyperparameters. The code to easily create VAEs is available on GitHub, where a package is offered to build VAE models by specifying only the number of channels for each convolutional layer.

The model training was carried out using a loss function called BetaLoss, which combines two components: reconstruction loss and latent loss weighted by a \(\beta\) parameter. This function is defined as:

\[\mathcal{L}_{\text{BetaVAE}} = \mathcal{L}_{\text{rec}} + \beta \cdot \mathcal{L}_{\text{latent}}\]

The \(\beta\) parameter controls the balance between reconstruction quality and latent space regularization.
A value of \(\beta < 1\) favors better image reconstruction, while a value of \(\beta > 1\)
prioritizes latent space regularization by applying a higher penalty on KL divergence.

Implemented Models

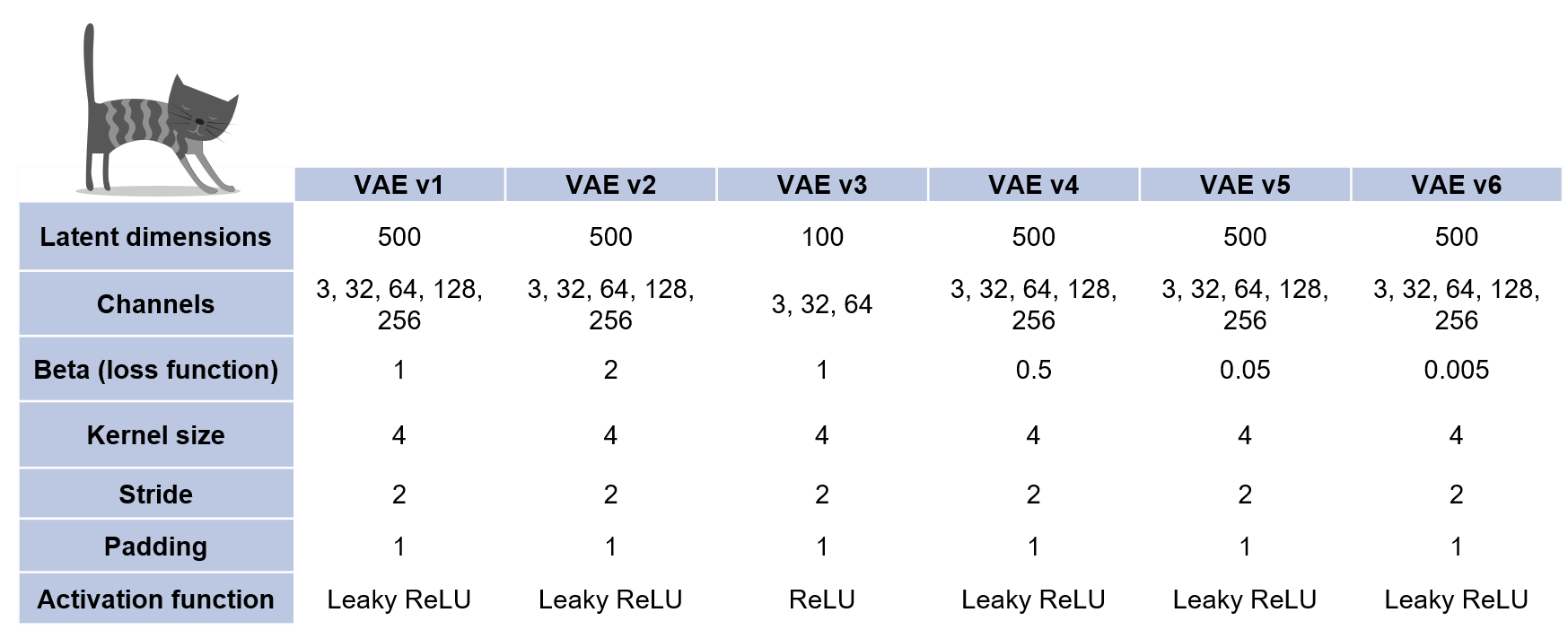
Six versions of VAE were tested. The models v1, v2, v4, v5, and v6 share the same architecture, with the only difference being the BetaLoss function.

In the v1 model, the standard VAE loss function is used with a \(\beta = 1\). In the v2 model, the \(\beta\) value is doubled, i.e., \(\beta = 2\). In the v4, v5, and v6 models, the \(\beta\) value is progressively reduced to \(\beta = 0.5\), \(\beta = 0.05\), and \(\beta = 0.005\) respectively. In the v3 model, a simpler architecture was used, with fewer layers and parameters.

Experiments

To select the best model, we analyzed some samples of the generated images and evaluated the quality of the reconstructions (i.e., how blurry or sharp the reconstructed images look) and the quality of the interpolations (i.e., how smooth and realistic the transitions between two images are).

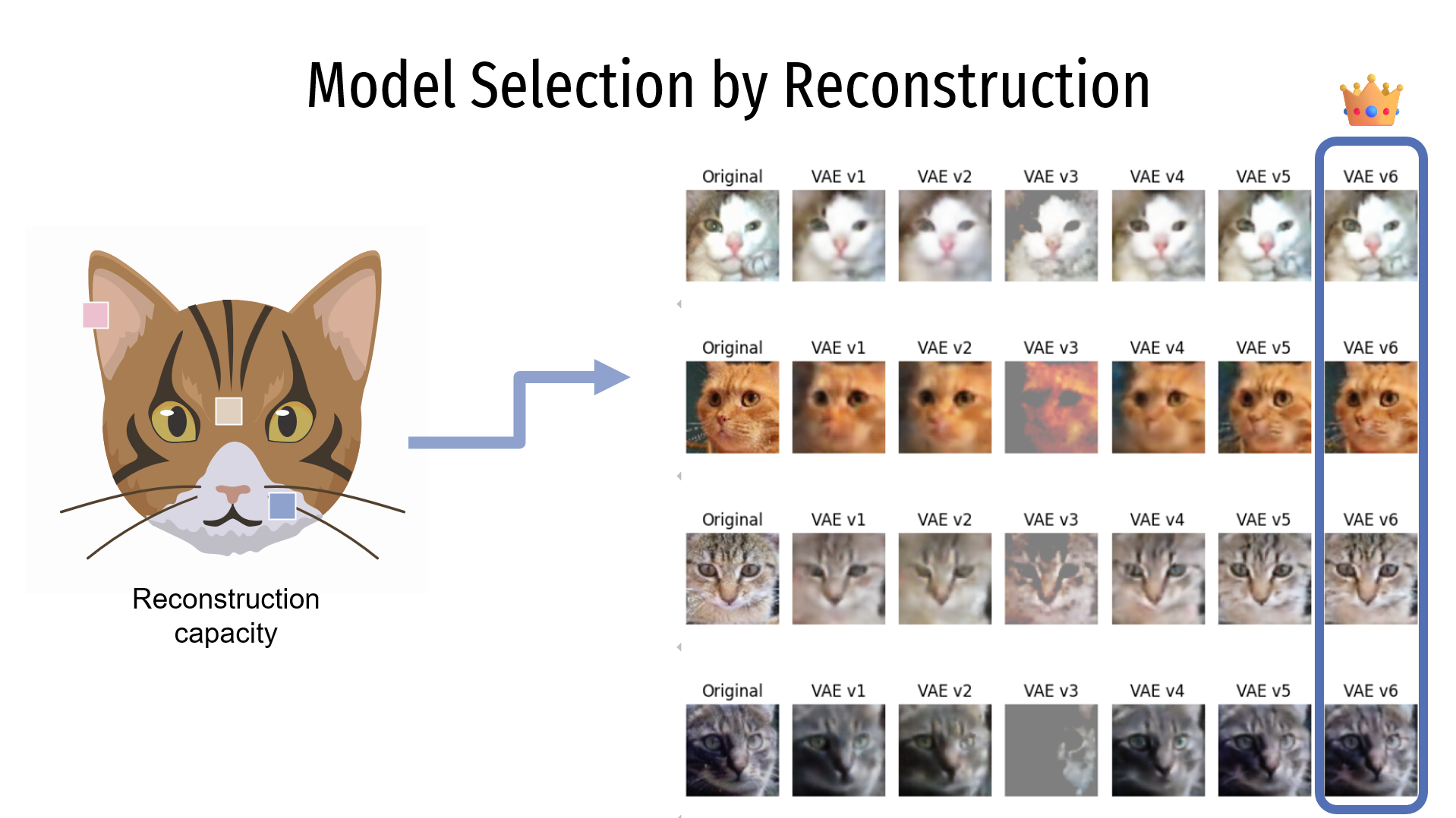
For the reconstruction, the image shows the evaluated models in the columns, with the rows representing different images from the dataset. The first column corresponds to the original image, and each of the following columns represents the reconstruction generated by each model. It can be seen that the VAEv6 model produces the best reconstruction.

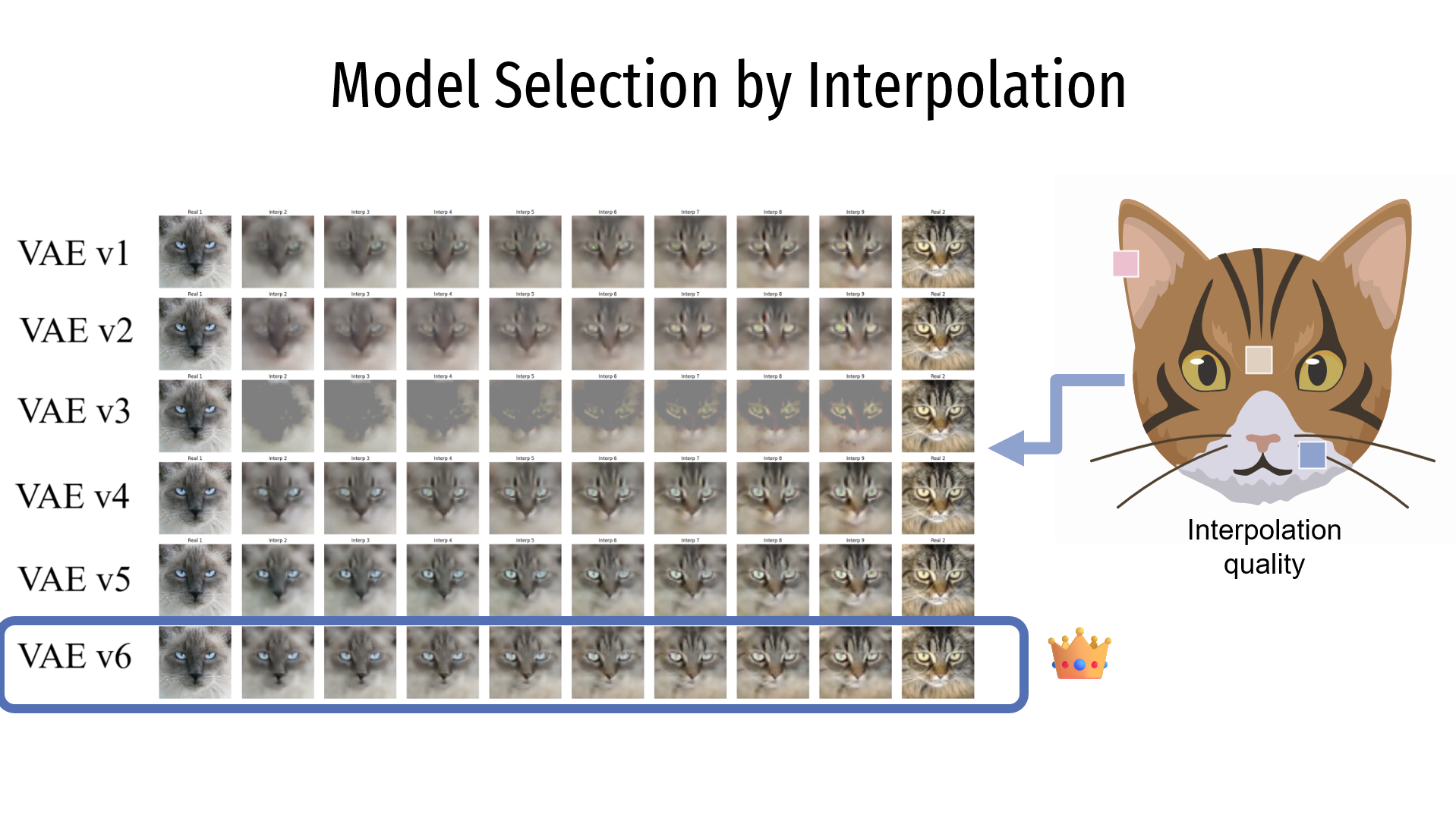
For the interpolation, the image shows each row corresponding to a different model. The first and last columns show two original images from the dataset, while the intermediate columns represent the transitions generated between the two images. Again, it is observed that the VAEv6 model generates the best interpolations.

Conclusions

From the experiments, we observed that increasing the \(\beta\) value, which implies greater latent space regularization, negatively affects the reconstruction ability of the images. Therefore, models v1 and v2 were discarded.

Instead, reducing the \(\beta\) value significantly improved reconstruction performance without substantially compromising interpolations. For this reason, model v6 (\(\beta = 0.005\)) was selected as the best, as it offers the best reconstruction quality without losing proper latent space regularization.

As for model v3, which features a simpler architecture with fewer parameters, this simplicity proved insufficient to capture the complexity of cat face images. Therefore, it was deemed unfeasible for use in this context.