Random Circle Problem

In this mathematical puzzle, we’ll exercise our minds with basic probability and geometry, making it an ideal exercise for learners of all levels. Brace yourself for a short yet thought-provoking solution that will challenge your understanding of probabilities within probabilities. Are you ready to take on this captivating challenge? Let’s dive right in!

Statement

Given a circle $C_a$​ of radius $a$ centered at the origin, inscribed in a square $S$ of side $2a$.

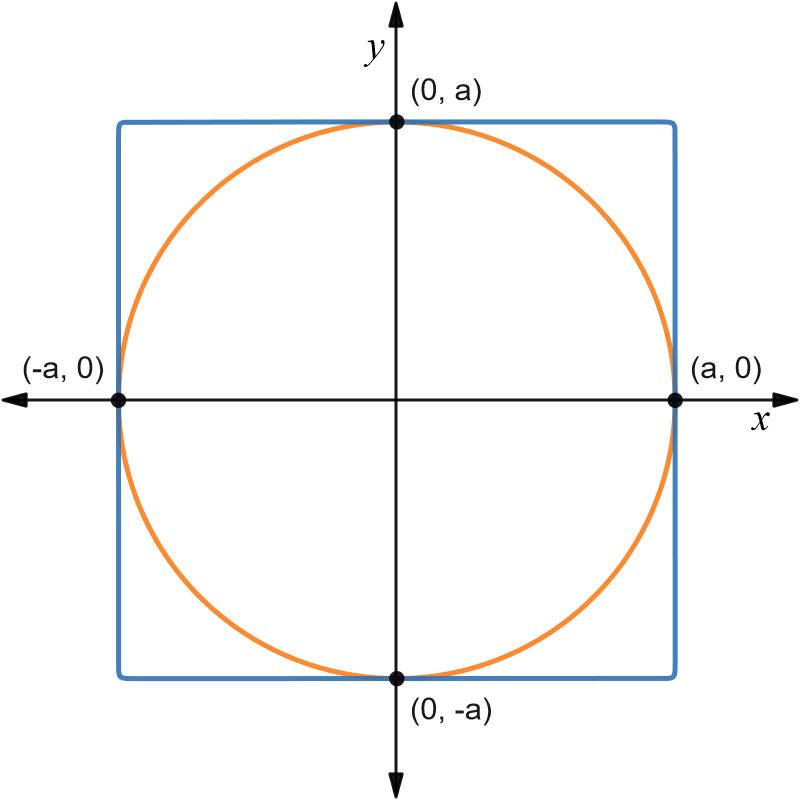A circle $C_a$ inscribed in a square $S$.

Consider a random variable $B \sim \text{Uniform}(0, a)$, the random variables $X, Y \sim \text{Uniform}(-a, a)$, the outcomes $b \in B$, $x \in X$ and $y \in Y$, and a real number $\rho \in [0, 1)$.

Find the probability of observing an outcome $b$ such that the probability of a circle $C_b$ with radius $b$ centered at $P = (x, y)$ being fully contained within $C_a$ is greater than $\rho$.

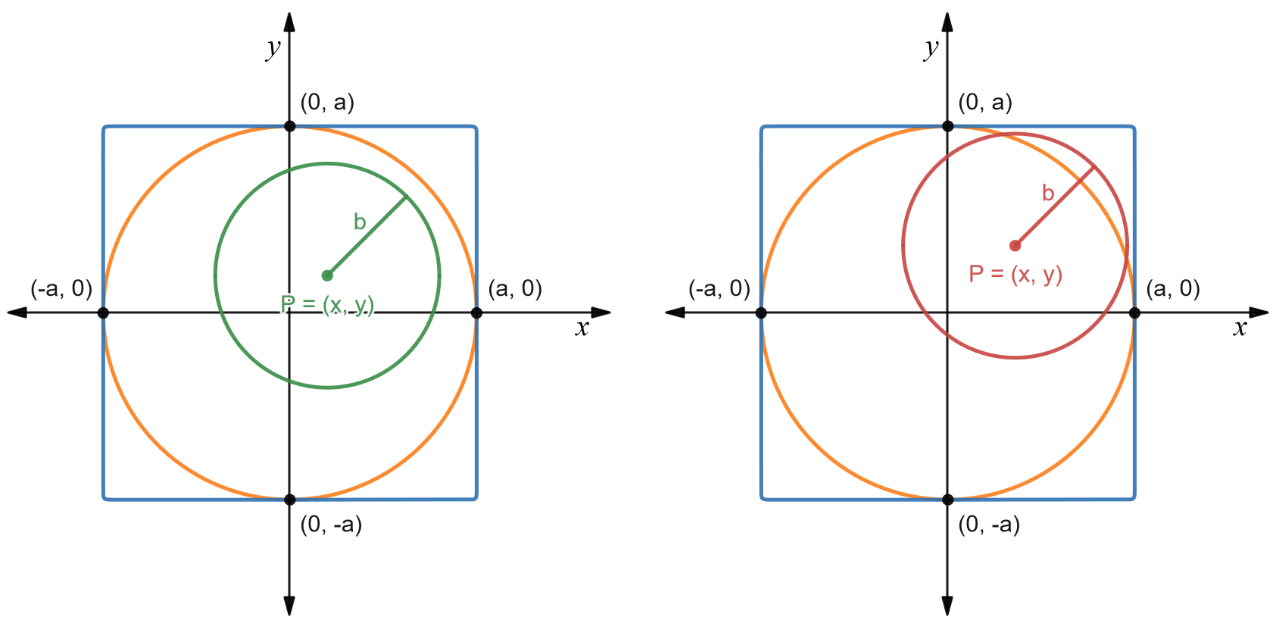
Example of sampling random $C_b$ circles for a fixed value of $b$.

That is, find the probability of observing an outcome $b$ such that:

\[\mathbb{P}\{C_b \subseteq C_a\} > \rho\]

Note that $C_b$ is not necessarily fully contained in $S$.

Solution

Probability of $C_b \subseteq C_a$

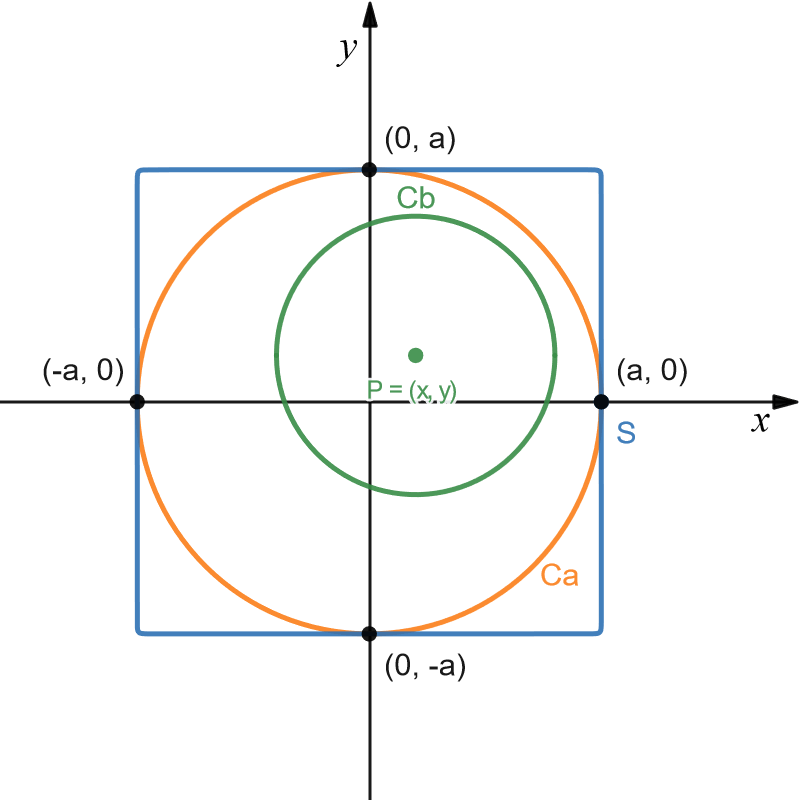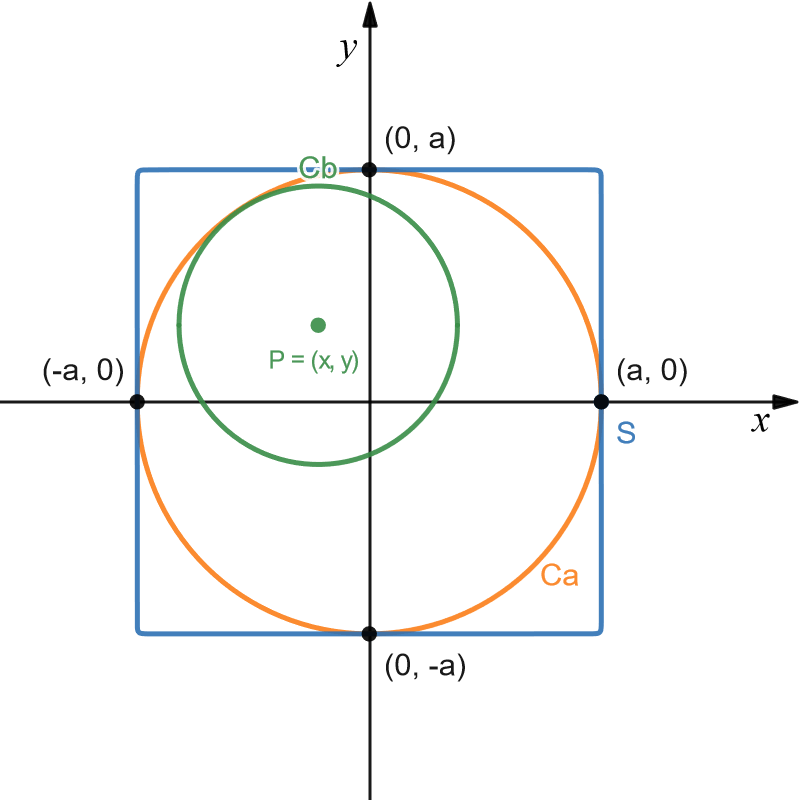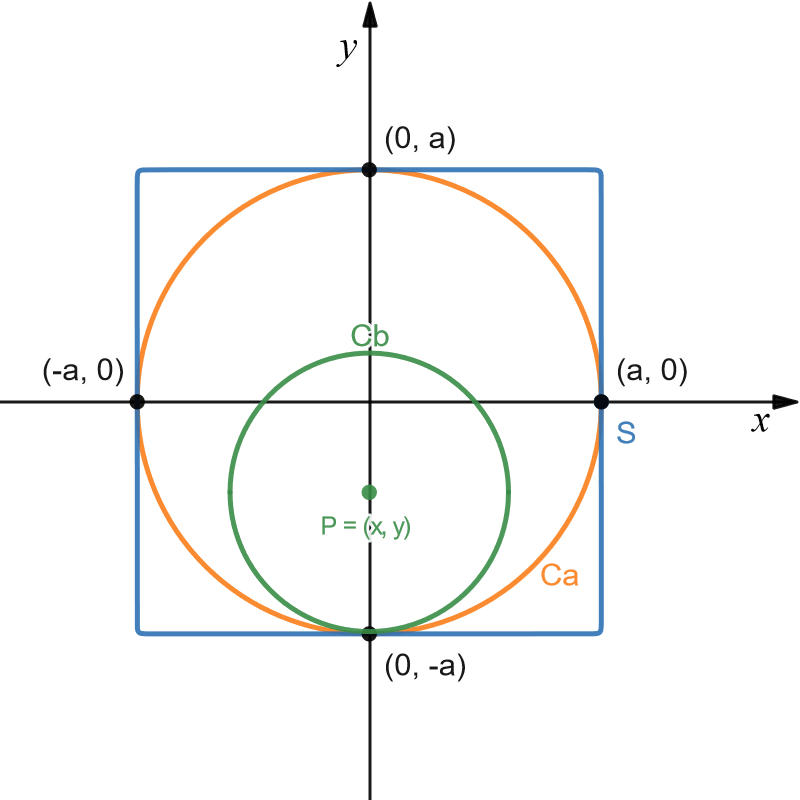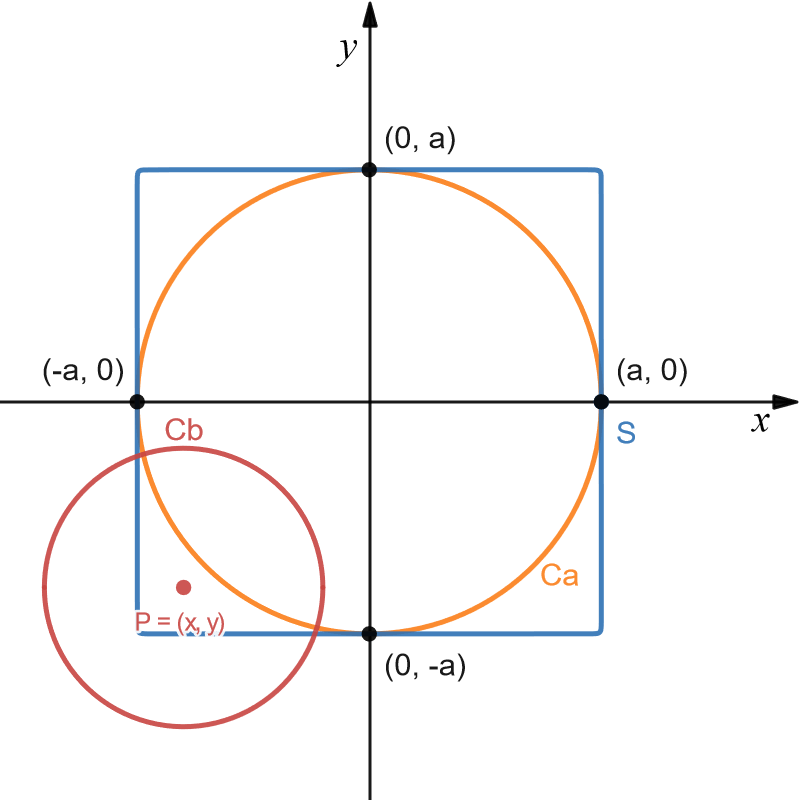
Let’s consider a point $P$ inside the square $S$. The circle $C_b$ is described by the circumference of radius $b$ centered at $P$. If $C_b$ is fully contained in $C_a$, then $P$ must be inside $C_a$, and the distance between $P$ and the circumference of $C_a$ must be greater than $b$.

This means that $C_b$ is fully contained in $C_a$ if and only if its center $P$ is inside the circle $C_{ab}$ of radius $a-b$ centered at the origin.

Then the probability that $C_b$ is fully contained in $C_a$ is the ratio between the area of $C_{ab}$ and the area of $S$:

\[\mathbb{P}\{C_b \subseteq C_a\} = \frac{\pi (a-b)^2}{(2a)^2} = \frac{\pi}{4} \frac{(a-b)^2}{a^2}\]

Probability of $\mathbb{P}(C_b \subseteq C_a) > \rho$

We are looking for the probability of observing an outcome $b$ such that

\[\mathbb{P}\{C_b \subseteq C_a\} > \rho\]

that is

\[\frac{\pi}{4} \frac{(a-b)^2}{a^2} > \rho\]

By clearing $b$ from the inequality, we get

\[b < a \left(1 - \sqrt{\frac{4}{\pi} \rho }\right)\]

As $B$ is a uniformly distributed within the interval $[0, a]$, its probability density function is:

\[f(x) = \begin{cases} \frac{1}{a} &\quad\text{if } 0 \le x \le a\\ 0 &\quad\text{otherwise.} \\ \end{cases}\]

Then the probability of $b < a \left(1 - \sqrt{\frac{4}{\pi} \rho }\right)$ is simply the area of the rectangle with height $\frac{1}{a}$ and base $a \left(1 - \sqrt{\frac{4}{\pi} \rho }\right)$

\[P\Big\{b < a \left(1 - \sqrt{\frac{4}{\pi} \rho }\right)\Big\} = \frac{1}{a} \cdot a \left(1 - \sqrt{\frac{4}{\pi} \rho }\right) = 1 - \sqrt{\frac{4}{\pi} \rho }\]

Therefore, the probability of observing an outcome $b$ such that $\mathbb{P}${$C_b \subseteq C_a$}$ > \rho$ is

\[\therefore \mathbb{P}\Big\{\mathbb{P}\{C_b \subseteq C_a\} > \rho\Big\} = 1 - \sqrt{\frac{4}{\pi} \rho }\]