ElectriPy
Welcome to ElectriPy, a powerful and interactive electrostatic simulator designed to help you gain an intuitive understanding of how electric fields and charges behave. Created as a personal project to visualize the principles of physics, ElectriPy lets you play with electrons and protons, observing how the electric field changes as you add more charges to the simulation.
ElectriPy was developed as a user-friendly and engaging tool to facilitate the exploration of electrostatics. Unlike precise calculators, ElectriPy emphasizes simulation and learning through interactive play. Whether you are a student, an educator, or simply someone curious about the fascinating world of physics, this simulator is here to spark your interest and deepen your understanding of electric fields.
You can find ElectriPy source code on GitHub.
Installation
Getting started with ElectriPy is easy. You’ll need to have Python 3.10 (or above) and pip installed. Once you’ve met these requirements, simply install Numpy, Pygame and the ElectriPy package using the following commands:
1
2
3
$ pip install numpy
$ pip install pygame
$ pip install electripy
You are all done! To start the simulation type:
1
$ python -m electripy
Features and Controls
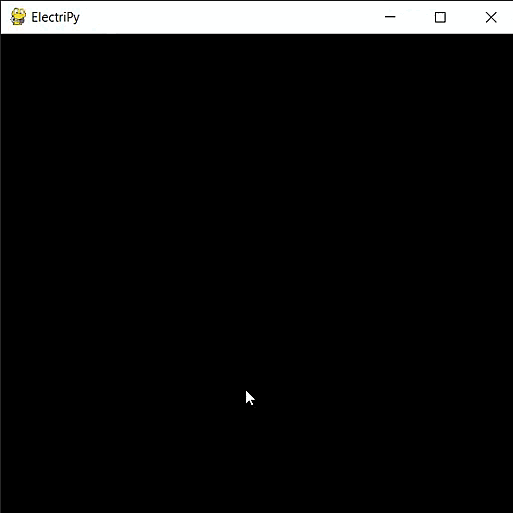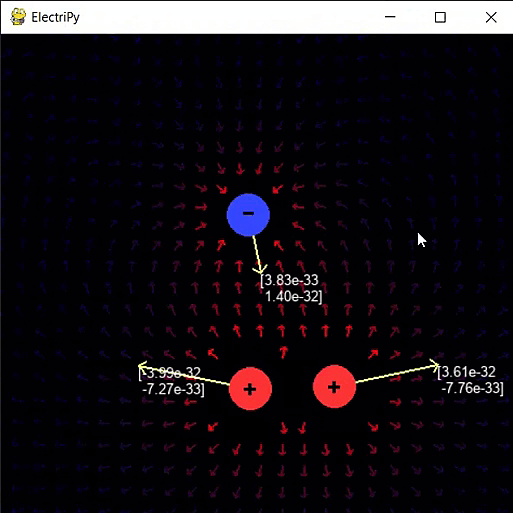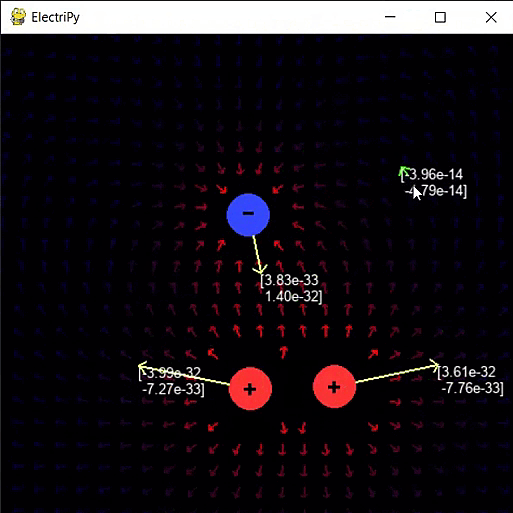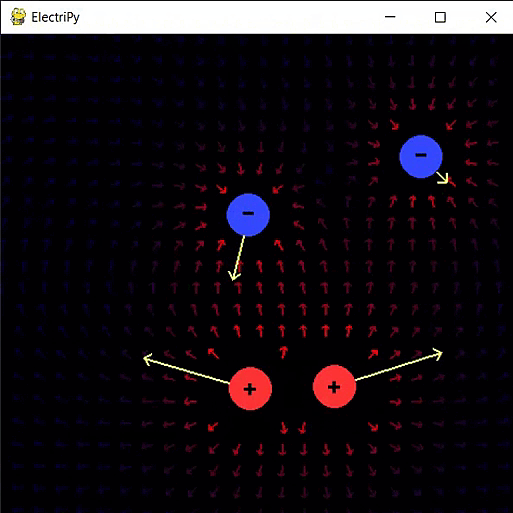
- right click to add an electron
- left click to add a proton
- CTRL + Z to remove last charge added
- CTRL + Y to add last charge removed
- R to remove all charges from screen
- E to show/hide the electric field
- + to increment the electric field brightness
- - to decrement the electric field brightness
- F to show/hide electric force vectors
- M to show/hide electric field vector at cursor position
- SPACE to show/hide vectors components
Physics
This section explains the physics of ElectriPy. If you want to see its implementation on Python you can go to ElectriPy physics package on GitHub. While following the logic and formulas below it is important to consider that all charges are point charges (i.e. their mass is negligible) and are at rest.
Electric force calculation
Two point charges
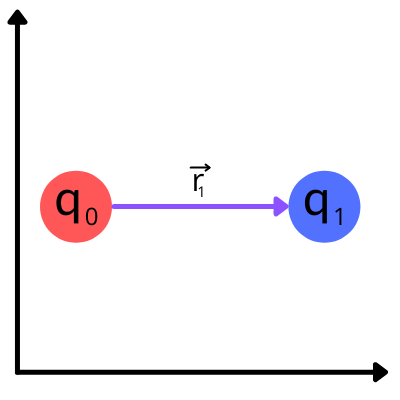
Imagine we have a plane with two point charges at rest, \(q_0\) and \(q_1\):
\(q_0\) exerts an electric force \(\vec{\textbf{F}}_0\) on \(q_1\), and \(q_1\) exerts an electric force \(\vec{\textbf{F}}_1\) on \(q_0\). These electric forces have the same magnitude but opposite direction. We can calculate the electric forces’ magnitude with Coulomb’s law:
\[F = \frac{1}{4\pi\varepsilon_0}\frac{\|q_0q_1\|}{r^2}\]Nevertheless, we need to find the electric forces vector, not only their magnitude. To simplify our task we are going to analyze the electric force exerted only on \(q_0\), which is \(\vec{\textbf{F}}_1\). Since we now have one force, we will call it \(\vec{\textbf{F}}\). In other words, \(\vec{\textbf{F}}_1\) = \(\vec{\textbf{F}}\).
\(\vec{\textbf{r}}\) is a vector that goes from \(q_0\) to \(q_1\). However is more useful to find \(\hat{\textbf{r}}\), which has the same direction as \(\vec{\textbf{r}}\) but it is a unit vector. \(\hat{\textbf{r}}\) can be easily calculated by scaling \(\vec{\textbf{r}}\) by the inverse of its norm: \(\hat{\textbf{r}}=\frac{\vec{\textbf{r}}}{\|\vec{\text{r}}\|}\)
In this scenario, \(\vec{\textbf{F}}\) can be calculated as \(F\hat{\textbf{r}}\). This is not always the case though. What would happen if \(q_1\) was a positive charge?:
Here the electric force has changed, it is now calculated as \(\vec{\textbf{F}}=-F\hat{\textbf{r}}\).
As we see, the direction of \(\vec{\textbf{F}}\) does not only depend on \(q_0\) and \(q_1\) magnitude but also on their sign. By analyzing some other examples we can deduce that \(\vec{\textbf{F}}\) is:
\[\vec{\textbf{F}}=-\frac{1}{4\pi\varepsilon_0}\frac{q_0q_1}{r^2}\hat{\textbf{r}}\]Multiple point charges
Now let’s imagine that we have three point charges:
If we look at \(q_0\) we can observe that it suffers a force \(\vec{\textbf{F}}_1\) exerted by \(q_1\) and a force \(\vec{\textbf{F}}_2\) exerted by \(q_2\). The net force exerted on \(q_0\) is \(\vec{\textbf{F}}\), which is the sum of \(\vec{\textbf{F}}_1\) and \(\vec{\textbf{F}}_2\). This is called the Principle of Superposition and it is fulfilled for any charge distribution.
Given a distribution of \(n\) charges \(\\{q_0,q_1,\ldots,q_n\\}\), the electric force exerted on \(q_0\) is \(\vec{\textbf{F}}\) and can be calculated as:
\[\vec{\textbf{F}}=\sum_i\vec{\textbf{F}}_i\]After replacing \(\vec{\textbf{F}}_i\) by its value:
\[\vec{\textbf{F}}=\sum_i-\frac{1}{4\pi\varepsilon_0}\frac{q_0q_i}{r_i^2}\hat{\textbf{r}}_i\]We can optimize this by taking the constants values outside of the summatory:
\[\vec{\textbf{F}}=-\frac{1}{4\pi\varepsilon_0}\sum_i\frac{q_0q_i}{r_i^2}\hat{\textbf{r}}_i\]We have arrived to a formula for calculating the electric net force of a given charge on an electric field distribution.
Electric field calculation
The electric field is defined mathematically as a vector field that associates to each point in space the force per unit of charge exerted on an infinitesimal positive test charge at rest at that point.
Given a test charge \(q_0\) at a point \(P(x,y)\) and a charge distribution \(\\{q_1,q_2,\ldots,q_n\\}\), we can calculate the electric field at \(P\) position as:
\[\vec{\textbf{E}}=\frac{\vec{\textbf{F}}}{q_0}\]Where \(\vec{\textbf{E}}\) is the electric field vector at position \(P\), and \(\vec{\textbf{F}}\) is the electric force exerted on \(q_0\) by the charge distribution. If we replace \(\vec{\textbf{F}}\) by its value we get the formula to calculate the electric field at any point:
\[\vec{\textbf{E}}=-\frac{1}{4\pi\varepsilon_0}\sum_i\frac{q_i}{r_i^2}\hat{\textbf{r}}_i\]Where \(r_i\) is the distance from the point \(P\) to the charge \(q_i\) and \(\hat{\textbf{r}}_i\) is the unit vector with the same direction as \(\vec{\textbf{r}}_i\), the vector that goes from \(P\) to the charge \(q_i\).
Conclusion
ElectriPy is an engaging and user-friendly electrostatic simulator that allows you to explore the intriguing world of electric fields and charges. Through interactive play and visualizations, ElectriPy offers a platform to experiment with point charges, observe electric field interactions, and gain valuable insights into fundamental physics concepts.
As a tool for learning and teaching, ElectriPy serves as an excellent resource for students, educators, and enthusiasts alike. By interacting with electrons and protons and manipulating electric fields, you can develop an intuitive understanding of how charges behave and how their interactions shape the electric field.
While ElectriPy may not be as complex as some specialized simulation tools, its simplicity allows for an accessible and enjoyable learning experience. It aims to spark curiosity, enhance intuition, and provide a starting point for further exploration of electrostatics.
Show Your Support
If you enjoyed using ElectriPy and found value in its educational features, we encourage you to consider giving it a star on GitHub. Your support motivates us and shows appreciation for the effort put into creating this interactive electrostatic simulator.
Feel free to share ElectriPy with others who might benefit from this hands-on learning experience. Together, we can inspire a deeper appreciation and understanding of electric fields and their fascinating behavior.
Thank you for being a part of the ElectriPy community, and we hope you find value in your exploration of electric fields with this interactive tool. Happy simulating!