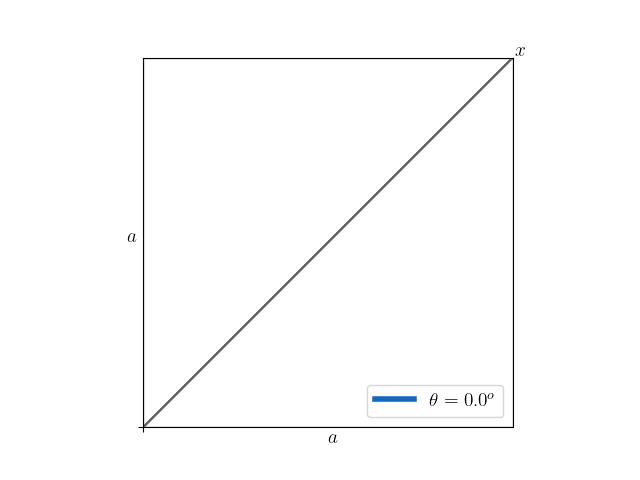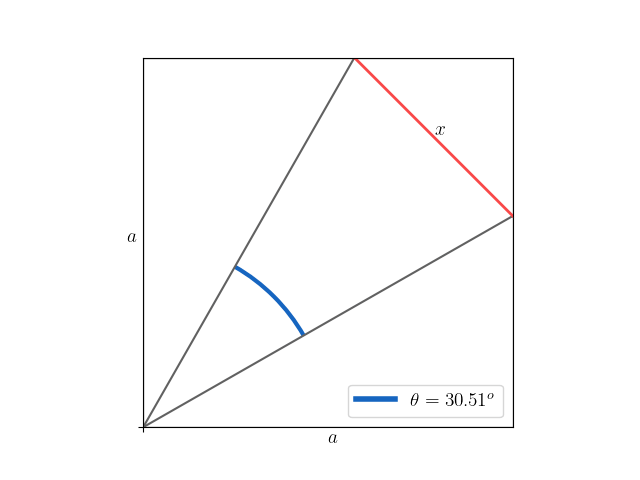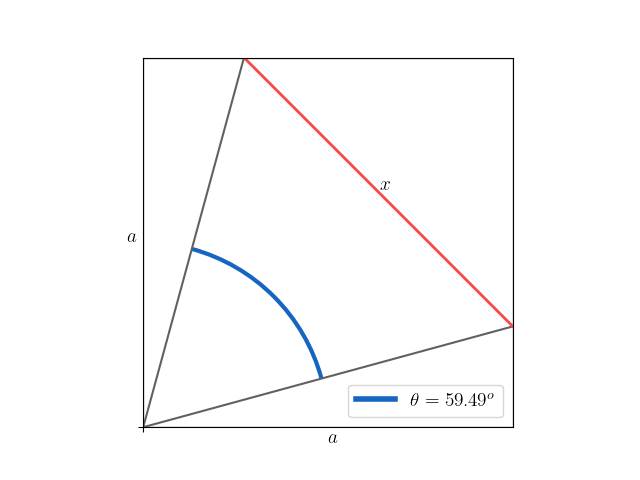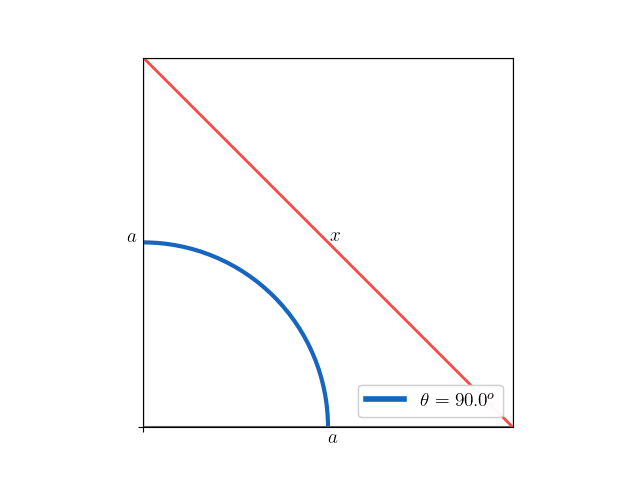
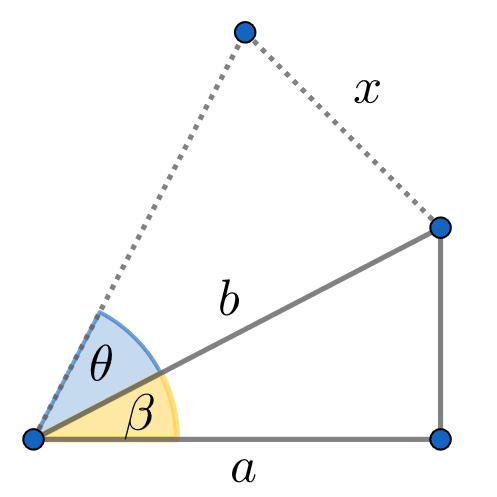
The Triangle Problem

Discover a simple yet engaging trigonometry problem that involves an isosceles triangle within a square. Your goal is to determine the length of the triangle’s base given the angle of the isosceles triangle and the side length of the square. Sharpen your problem-solving skills and enjoy exploring the relationship between angles and side lengths in this intriguing challenge. Have fun uncovering the solution!

Statement

Find a function \(f\) of \(a\) and \(\theta\) with domain

\[f : \mathbb{R}^{+} \times (0, \frac{\pi}{2}] \rightarrow \mathbb{R}^{+}\]

such that \(f(a, \theta) = x\).

For example, consider \(a = 1\) and \(\theta = \frac{\pi}{2}\), then the value of \(x\) is

\[x = f(1, \frac{\pi}{2}) = \sqrt{1^2 + 1^2} = \sqrt{2}\]

Solution

Defining \(x\) in terms of \(b\)

First, let’s define a new variable \(b\) equal to the length of the two remaining sides of the triangle

We can now write \(x\) in terms of \(b\) and \(\theta\)

\[\begin{align*} \sin(\frac{\theta}{2}) &= \frac{x/2}{b}\\ x &= 2 b \sin(\frac{\theta}{2}) \end{align*}\]

Finding \(b\) value

Now we have to find the value of \(b\)

\[\begin{align*} \cos(\beta) &= \frac{a}{b}\\ b &= \frac{a}{\cos(\beta)} \end{align*}\]

To calculate \(\cos(\beta)\), keep in mind that \(2\beta + \theta = \frac{\pi}{2}\)

\[\begin{align*} 2\beta + \theta &= \frac{\pi}{2}\\ 2\beta &= \frac{\pi}{2} - \theta\\ \beta &= \frac{\frac{\pi}{2} - \theta}{2} \end{align*}\]

Then

\[\begin{align*} \cos(\beta) &= \cos(\frac{\frac{\pi}{2} - \theta}{2})\\ &= \cos(\frac{\theta - \frac{\pi}{2}}{2})\\ &= \cos(\frac{\theta}{2} - \frac{\pi}{4})\\ &= \cos(\frac{\theta}{2}) \cos(\frac{\pi}{4}) + \sin(\frac{\theta}{2}) \sin(\frac{\pi}{4})\\ &= \frac{1}{\sqrt{2}} [\cos(\frac{\theta}{2}) + \sin(\frac{\theta}{2})] \end{align*}\]

and

\[b = \frac{a\sqrt{2}}{\cos(\frac{\theta}{2}) + \sin(\frac{\theta}{2})}\]

Finding \(x\)

\[\begin{align*} x &= 2 b \sin(\frac{\theta}{2})\\ &= 2 \sqrt{2} a \frac{\sin(\frac{\theta}{2})}{\sin(\frac{\theta}{2}) + \cos(\frac{\theta}{2})}\\ &= \sqrt{8} a (\frac{\sin(\frac{\theta}{2}) + \cos(\frac{\theta}{2})}{\sin(\frac{\theta}{2})})^{-1}\\ &= \sqrt{8} a (1 + \frac{\cos(\frac{\theta}{2})}{\sin(\frac{\theta}{2})})^{-1}\\ &= \sqrt{8} a \frac{1}{1 + \cot(\frac{\theta}{2})}\\ \therefore x &= \frac{\sqrt{8} a}{1 + \cot(\frac{\theta}{2})} \end{align*}\]