La importancia un buen generador de números aleatorios en una simulación
En este post se expone el trabajo integrador de la materia Simulación de la carrera de Ingeniería en Sistemas de Información de la Universidad Tecnológica Nacional, Facultad Regional de Mendoza. El trabajo fue realizado por Micaela Estrella y Dylan Tintenfich en el año 2023.
Introducción
Una variable aleatoria es una función que transforma un conjunto de números aleatorios en una sucesión que se corresponde con una distribución de probabilidad. Por lo tanto, la eficacia de este generador está condicionada por la calidad del generador de números aleatorios. No solo se trata de que los números aleatorios sean probabilísticamente de distribución uniforme e independientes, sino que el generador tenga un ciclo suficientemente amplio para obtener resultados verosímiles, sin que esto signifique que genere un impacto importante en el rendimiento del sistema. Por lo cual, en el siguiente informe nos proponemos analizar dicha influencia de los números aleatorios en la generación de variables aleatorias a partir de estos, desarrollando cada método desde cero y comparando los resultados de múltiples situaciones distintas.
Objetivos del proyecto
- Desarrollar generadores de variables aleatorias eficaces que cubran un amplio espectro de distribuciones de probabilidad
- Probar la dependencia de estos de la calidad del generador de números aleatorios
- Desarrollar algoritmos que siempre generen variables aleatorias de calidad y de bajo impacto en el sistema
Alcances del proyecto
El proyecto será desarrollado en su totalidad en Python. Se pueden distinguir las etapas expuestas a continuación.
Desarrollo de generadores de números aleatorios: Estos se desarrollarán de forma totalmente manual para tener total control de la calidad de los mismos. Se crearán generadores tanto congruenciales lineales como de cuadrados medios. De los primeros se brindará la opción de obtener generadores multiplicativos y mixtos y métodos para probar si son de ciclo completo.
Validación de generadores de números aleatorios: Se desarrollarán pruebas para validar la uniformidad e independencia estadísticas de las sucesiones de números obtenidas con los generadores antes dichos.
Desarrollo de generadores de variables aleatorias: Estos transformarán la sucesión de un generador especificado en una sucesión de variables aleatorias según una distribución a elección.
Validación de generadores de variables aleatorias: Se probarán los generadores de variables aleatorias con distintas sucesiones de números aleatorios para analizar el impacto de la calidad del primero en el segundo. Para esto, se realizará una simulación y se analizará el impacto en el resultado de la misma obtenido al definir distintos generadores de números aleatorios.
Implementación en Python
A continuación se explicarán los generadores de números pseudoaleatorios, los generadores de variables aleatorias y las pruebas de aletoriedad implementados en Python.
El código fuente puede encontrarse en el siguiente repositorio de GitHub.
Generador de números pseudoaleatorios
Para facilitar la creación de generadores de números pseudoaleatorios a lo largo del trabajo práctico, se decidió abstraer el concepto de generador de números aleatorios con la clase Generator. Todos los generadores son subclases de Generator y deben implementar el método next(), el cual retorna el siguiente número aleatorio. También debe implementar el método get_xn_sequence() y el método get_random_numbers(), los cuales devuelven la secuencia entera de números pseudoaleatorios \(\{\mu_0, \mu_1, \dots, \mu_n\}\) y la secuencia de reales generados \(\{x_0, x_1, \dots, x_n\}\) respectivamente. Por último deben implementar el método verify_parameters(), que verifica la validez de los parámetros del generador.
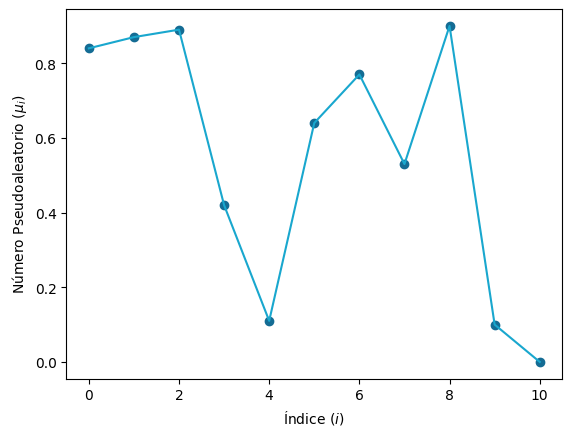
Además, todas las subclases de Generador cuentan con el método plot_random_numbers(), que grafica la secuencia de números pseudoaleatorios en el plano \(xy\), donde el eje \(x\) representa el índice \(i\) del número pseudoaleatorio, y el eje \(y\) representa el valor del número psuedoaleatorio \(\mu_i\). Éste método admite el parámetro join_points, que en el caso de ser verdadero, une los puntos entre los números pseudoaleatorios, facilitando la visualizacion del orden de la secuencia \(\mu_1, \mu_2, \dots, \mu_n\) generada.
Los generadores concretos implementados son:
MixedCongruentialGenerator(generador congruencial lineal mixto)MultiplicativeCongruentialGenerator(generador congruencial lineal multiplicativo)MiddleSquareGenerator(generador de cuadrados medios)DependentGenerator(generador dependiente)
Estos serán explicados con mayor detalle a continuación.
Generadores congruenciales lineales
LinearCongruentialGenerator es una clase abstracta que representa el concepto de generador congruencial lineal. Se concreta en dos generadores, a saber, el MultiplicativeCongruentialGenerator y el MixedCongruentialGenerator.
Los generadores congruenciales lineales se definen denotando la relación recursiva de la siguiente manera:
\(x_{n+1} = \left( a x_n + b \right)\bmod m\) \(\mu_n = \frac{x_n}{m}\)
donde \(x_n\) es la n-ésimo término del generador, \(x_0\) es el primer término llamado semilla, \(\mu_n\) es el n-ésimo número aleatorio generado, \(m\) es el módulo, \(a\) el elemento multiplicativo y \(b\) es el elemento aditivo. El número aleatorio se calcula como:
La clase abstracta cuenta con un único método a implementar obligatoriamente: has_max_sequence(), que devuelve un booleano que indica si el generador es de ciclo completo. Por su parte, implementa los métodos que hereda de Generator y lanza un error si se intenta crear un Generador con parámetros inválidos. Por ejemplo, impide que se asigne al elemento multiplicativo un número superior al módulo.
Generador de cuadrados medios
Los generadores de cuadrados medios serán instancias de la clase MiddleSquareGenerator. Su constructor recibe los parámetros:
- \(k > 0\) - es el número de dígitos de los números aleatorios resultantes
- \(x_0 > 0\) - es la semilla o valor inicial
Generador dependiente
Para evaluar el impacto de un mal generador en la creación de variables aleatorias, se desarrolló un generador dependiente, es decir, un generador de números aleatorios que no cumple con la condición de independencia. El generador esta implementado por la clase DependentGenerator, y su secuencia de términos \(X\) se define como
Donde \(x_0\) es la semilla del generador (\(x_0 > 1\)) y \(\mu_n\) es el n-ésimo número aleatorio generado.
1
2
3
from src.random_number import DependentGenerator
DependentGenerator(seed=10).get_random_numbers()
[1.0, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1, 0.0]
Como podemos observar, el generador cumple con uniformidad ya que todo los números aleatorios generados tienen igual probabilidad de ocurrencia, sin embargo, hay una clara dependencia entre un número aleatorio \(\mu_i\) y su anterior \(\mu_{i-1}\).
Ejemplos
Generador congruencial mixto de ciclo completo
A continuación se presenta la implementación del siguiente generador:
\(x_{i+1} = \left( 4x_i + 7 \right)\bmod 9\) \(x_0 = 9\)
con una semilla de valor 9; se imprime la secuencia de términos \(X = \{x_0, x_1, \dots, x_n\}\) y se indica si el generador es de ciclo completo.
1
2
3
4
5
6
7
8
9
10
11
12
from src.random_number import MixedCongruentialGenerator
from src.utils import print_markdown
generator = MixedCongruentialGenerator(seed=8,a=4,b=7,m=9)
print_markdown(f"La secuencia de $$ x_i $$ es: $$ {generator.get_xn_sequence()} $$")
print_markdown(f"La longitud del generador es: $$ {len(generator)} $$")
if generator.has_max_sequence():
print_markdown(f"El generador tiene ciclo completo")
else:
print_markdown("El generador tiene ciclo incompleto")
La secuencia de \(x_i\) es: \([8, 3, 1, 2, 6, 4, 5, 0, 7]\)
La longitud del generador es: \(9\)
El generador tiene ciclo completo
Notemos que, como el generador es de ciclo completo, la longitud de la secuencia de números generada coincide con el módulo \(m\).
Generador congruencial multiplicativo
Se presenta el generador:
\[x_{i+1} = 4x_i \mod 9\]con una semilla de 8, imprimiéndose tanto su secuencia de términos \(X = \{x_0, x_1, \dots, x_n\}\) como la secuencia de números aleatorios \(\mu = \{\mu_0, \mu_1, \dots, \mu_n\}\).
1
2
3
4
5
6
from src.random_number import MultiplicativeCongruentialGenerator
generator = MultiplicativeCongruentialGenerator(seed=8,a=4,m=9)
print_markdown(f"La secuencia de términos $$ X $$ es: $$ {generator.get_xn_sequence()} $$")
print_markdown(f"La secuencia de números aleatorios $$ \mu $$ es: $$ {generator.get_random_numbers()} $$")
La secuencia de términos \(X\) es: \([8, 5, 2]\)
La secuencia de números aleatorios \(\mu\) es: \([0.8888888888888888, 0.5555555555555556, 0.2222222222222222]\)
Gráfica de generador de cuadrados medios
Se presenta un generador que obtiene números de dos dígitos decimales y se la imprime en pantalla. Cabe recordar que el parámetro join_points por defecto es verdadero, y que por este motivo los puntos \((i,\mu_i)\) se unen con una línea.
1
2
3
4
from src.random_number import MiddleSquareGenerator
generator = MiddleSquareGenerator(k=2, seed=84)
generator.plot_random_numbers()
Pruebas estadísticas para validar la aleatoriedad de las sucesiones
El concepto de estas pruebas es representado con la clase abstracta RandomnessTest. Toda prueba tiene un constructor que recibe como parámetros el conjunto de números aleatorios a probar (random_numbers) y el estadístico relativo al nivel de significancia con que se realice la prueba (statistic) que deberá calculase manualmente. A su vez, todas deben implementar el método run_test() que utiliza todos estos datos para concluír en la aceptación o rechazo de la hipótesis e imprimir esto en pantalla haciendo uso de látex.
Las pruebas que se proveen son:
Tests de uniformidad
ChiSquaredTest(prueba de Chi Cuadrada, de Pearson o de Frecuencias)KolmogorovSmirnovTest(prueba de Kolmogorov-Smirnov)
Tests de independencia estadística
WaldWolfowitzRunsTest(prueba de rachas)
Prueba de la Chi Cuadrada
La clase ChiSquaredTest recibe una lista de números aleatorios denominada random_numbers, el número entero intervals que representa la cantidad de intervalos, y statistic que es el estadístico correspondiente al nivel de significancia de la prueba.
Sea \(\mu = \{\mu_1, \mu_2, \dots, \mu_n\}\) una secuencia de \(n\) números aleatorios y \(k\) la cantidad de intervalos, se genera \(k\) intervalos \([0, \frac{1}{k}), [\frac{1}{k}, \frac{2}{k}), \dots, [\frac{k-2}{k}, \frac{k-1}{k}), [\frac{k-1}{k}, 1]\) y se cuenta la cantidad de números aleatorios que caen en cada intervalo, obteniendo asi la frecuencia observada. El conjunto de números aleatorios \(\mu\) pasa la prueba si
\[X^2_0 = \sum_{i=1}^k \frac{({FO}_i - {FE}_i)^2}{{FE}_i} < X^2_{(\alpha, k-1)}\]donde \({FE}\) es la frecuencia esperada (\(\frac{n}{k}\)), \({FO}\) es la frecuencia observada y \(X^2_{(\alpha, k-1)}\) es el estadístico correspondiente al nivel de semejanza escogido.
Prueba de Kolmogorov-Smirnov
La clase KolmogorovSmirnovTest recibe como parámetros una lista de números aleatorios, random_numbers, y el estadístico correspondiente al nivel de semejanza escogido, statistic. Además cuenta con un método adicional llamado graph(), el cual grafica la secuencia de números aleatorios y la frecuencia absoluta esperada.
Dado el conjunto de números aleatorios ordenados \(\mu = \{\mu_1, \mu_2, \dots, \mu_n\}\) donde \(\mu_1 < \mu_2 < \dots < \mu_n\), se compara cada número aleatorio \(\mu_i\) con la función de probabilidad acumulada esperada \(\frac{i}{n}\) su semejanza. El conjunto de números aleatorios \(\mu\) pasa la prueba si
\[{max}\{|\frac{i}{n} - \mu_i|\} < D(\alpha, n)\]donde \(D(\alpha, n)\) es el estadístico correspondiente al nivel de semejanza escogido.
Prueba de rachas
La prueba de rachas o prueba de WaldWolfowitz es representada por la clase WaldWolfowitzRunsTest. Esta recibe como parámetros la lista de números aleatorios a probar random_numbers y el valor statistic que es el estadístico con el cual se comparará para determinar la aceptación o el rechazo de la hipótesis.
Para determinar las rachas, se agrupa los números aleatorios en dos categorías: positivos y negativos. Los números positivos son aquellos que son mayores que la media y los negativos son aquellos que son menores o iguales que esta. Luego se examina la secuencia de números aleatorios y se cuenta el número de cambios de categoría entre valores consecutivos. Cada cambio de categoría representa una racha.
Sea \(\mu = \{\mu_1, \mu_2, \dots, \mu_m\}\) el conjunto de \(m\) números aleatorios a probar, \(n_1\) el número de positivos y \(n_2\) el número de negativos; la clase WaldWolfowitzRunsTest entonces calcula
El conjunto de números aleatorios \(\mu\) pasa la prueba de rachas si
\[Z_b = \frac{b - \mu_b}{\sigma_b} < N_\alpha\]donde \(N_\alpha\) es el estadístico correspondiente al nivel de semejanza escogido.
Caso práctico
Se realizará las distintas pruebas de aletoriedad para la secuencia de números aleatorios \(\mu = \{0.84, 0.87, 0.89, 0.42, 0.11, 0.64, 0.77, 0.53, 0.9, 0.1, 0.0\}\)
1
2
3
from src import randomness_test
random_numbers = [0.84, 0.87, 0.89, 0.42, 0.11, 0.64, 0.77, 0.53, 0.9, 0.1, 0.0]
Prueba de la Chi Cuadrada
Realizaremos la prueba de la Chi Cuadrada con cuatro intervalos y un estadístico igual a \(7.779\)
1
randomness_test.ChiSquaredTest(random_numbers, intervals=4, statistic=7.779).run_test()
Prueba de Kolmogorov-Smirnov
Realizaremos la prueba Kolmogorov-Smirnov con un estadístico igual a \(0.35242\)
1
randomness_test.KolmogorovSmirnovTest(random_numbers, statistic=0.35242).run_test()
Prueba de Rachas
Realizaremos la prueba Rachas con un estadístico igual a \(1.645\)
1
randomness_test.WaldWolfowitzRunsTest(random_numbers, statistic=1.645).run_test()
Rachas: [0.84 0.87 0.89] [0.42 0.11] [0.64 0.77] [0.53] [0.9] [0.1 0. ]
\(b = 6\) (cantidad de rachas)
\(n_1 = 6\) (cantidad de números positivos)
\(n_2 = 5\) (cantidad de números negativos)
\(Z_{\alpha/2}\) = 1.645
\[Z_0 = \frac{b - \mu_b}{\sigma_b} = 0.029160592175990475\]-\(Z_{\alpha/2}\) \(\leq Z_0 \leq\) \(Z_{\alpha/2}\) \(\Rightarrow\) La hipótesis se acepta.
Generadores de variables aleatorias
El concepto de generador de variable aleatoria fue representado con la clase abstracta RandomVariable. Estos generadores transforman los números aleatorios de un generador (generator) en una secuencia de números con una distribución concreta.
Toda clase que hereda de RandomVariable debe implementar los métodos get_random_variables(), que retorna la sucesión de variables aleatorias en un arreglo, y next() que devuelve el siguiente valor de la sucesión.
Las distribuciones previstas para la generación de variables aleatorias son:
DiscreteRandomVariable(distribución discreta)UniformDiscreteRandomVariable(distribución uniforme y discreta)UniformContinuousRandomVariable(distribución uniforme y continua)AcceptanceRejectionVariable(distribución f según método de aceptación-rechazo)
Variables aleatorias de distribución discreta
Una variable aleatoria de distribución discreta o DiscreteRandomVariable es una función que asigna a cada número aleatorio \(\mu\) generado un valor de forma tal que el conjunto obtenido siga una distribución discreta.
El constructor de la clase recibe un generador de números aleatorios (generator) y los arreglos values y weights que representan la distribución discreta. values es el conjunto de salida de la función, es decir, los valores a asignar a los números aleatorios. Estos son tipo object, es decir, puede ser de cualquier tipo definido en python. weights es el conjunto de “pesos” de cada valor de values. El peso es un número real que representa la probabilidad de ocurrencia del valor. Se distingue del de probabilidad porque los pesos no necesariamente deben sumar 1. Las probabilidades de ocurrencia de los valores son calculadas normalizando los pesos, es decir, \(p_i = \frac{w_i}{\sum w_i}\).
Variables aleatorias de distribución uniforme
UniformDiscreteRandomVariable es una clase que hereda de DiscreteRandomVariable y que asigna a todos los valores de esta un mismo peso. Por lo tanto, su constructor recibe únicamente un generador de números aleatorios (generator) y el arreglo de valores (values).
Variables aleatorias de distribución uniforme continua
Una variable aleatoria de distribución uniforme continua o UniformContinuousRandomVariable asigna a cada número aleatorio generado un número real perteneciente al intervalo \([a, b]\), de forma tal que estos siguen una distribución uniforme.
El constructor de la clase recibe los parámetros generator que es un generador de números aleatorios, es decir, una subclase de Generator, y los números reales a y b, que definen el intervalo de salida como \([a,b]\).
Método de aceptación-rechazo
Para toda función no contemplada por las distribuciones anteriores, se define la clase AcceptanceRejectionVariable que obtiene una secuencia de valores según este método.
Los parámetros que recibe el constructor son:
generatorque es el generador con el que se obtiene el conjunto de números aleatorios de entrada. Es de tipoGenerator.aybque son los números reales que definen el intervalo de salida de la función, es decir, toda variable aleatoria generada pertenece al intervalo \([a,b]\)fdefinida como \(f: \mathbb{R} \rightarrow [0,\infty)\) es la función densidad de la variable aleatoria.gdefinida como \(g: \mathbb{R} \rightarrow [0,1]\) es una función que envuelve \(f\) en el intervalo \([a,b]\) y que se utiliza para la aceptación o rechazo de los valores.Mes el valor real \(M = \max{f(x)/g(x)}\)
Casos prácticos
A continuación se mostrarán casos prácticos donde se generan variables aleatorias. Para ello se utilizará el siguiente generador de números aleatorios.
1
2
3
from src.random_number import MixedCongruentialGenerator
generator = MixedCongruentialGenerator(seed=8,a=4,b=7,m=9)
Ejemplo de variable aleatoria de distribución uniforme
Se generará la variable aleatoria que indica de qué equipo de fútbol pertenecen distintos hinchas. En una entrevista realizada, se consiguieron los siguientes datos:
| Boca | River | Independiente | |
|---|---|---|---|
| Cantidad de Hinchas | 40 | 10 | 5 |
1
2
3
4
5
from src.random_variable import DiscreteRandomVariable
values = ["Boca", "River", "Independiente"]
weights = [40, 10, 5]
print("Las variables aleatorias generadas son:", DiscreteRandomVariable(generator, values, weights).get_random_variables())
1
Las variables aleatorias generadas son: ['River', 'Boca', 'Boca', 'Boca', 'Boca', 'Boca', 'Boca', 'Boca', 'River']
Ejemplo de variable aleatoria de distribución uniforme
A continuación mostraremos el ejemplo anterior, pero suponiendo de que hay la misma cantidad de hinchas de todos los equipos de fútbol.
1
2
3
4
from src.random_variable import UniformDiscreteRandomVariable
values = ["Boca", "River", "Independiente"]
print("Las variables aleatorias generadas son:", UniformDiscreteRandomVariable(generator, values).get_random_variables())
1
Las variables aleatorias generadas son: ['Independiente', 'Boca', 'Boca', 'Boca', 'River', 'River', 'River', 'Boca', 'Independiente']
Ejemplo de variable aleatoria de distribución continua
El siguiente ejemplo obtiene una secuencia de distribución uniforme con números entre 1 y 40.
1
2
3
4
from src.random_variable import UniformContinuousRandomVariable
randomvar = UniformContinuousRandomVariable(generator, a=1, b=40)
print(randomvar.get_random_variables())
1
[35.666666666666664, 14.0, 5.333333333333333, 9.666666666666666, 27.0, 18.333333333333332, 22.666666666666668, 1.0, 31.333333333333332]
Ejemplo de aplicación del método de aceptación rechazo.
Aplicaremos el método para obtener una variable cuya función de densidad sea \(f(x) = 2x\) para \(x \in [0, 1]\). Definimos \(g(x) = 1\) y \(M = 2\).
1
2
3
4
5
6
7
8
9
from src.random_variable import AcceptanceRejectionVariable
def f(x: float) -> float:
return 2 * x
def g(x: float) -> float:
return 1
print("Las variables aleatorias generadas son:", AcceptanceRejectionVariable(generator, a=0, b=1, f=f, g=g, M=2).get_random_variables())
1
Las variables aleatorias generadas son: [0.3333333333333333, 0.8888888888888888, 0.6666666666666666, 0.5555555555555556]
Implementación de una simulación
En esta sección, realizaremos una simulación del Algoritmo de Optimización de Colonia de Hormigas (ACO) para abordar el Problema del Viajante (TSP). Nuestro objetivo principal analizar el impacto de diferentes generadores de números aleatorios en los resultados obtenidos.
Algoritmo de optimización de colonia de hormigas
La Optimización de Colonia de Hormigas (ACO, por sus siglas en inglés) es un algoritmo metaheurístico inspirado en el comportamiento de búsqueda de alimento de las hormigas. Se utiliza comúnmente para resolver problemas de optimización, especialmente aquellos relacionados con la optimización combinatoria.
El algoritmo ACO se basa en el concepto de senderos de feromonas, que las hormigas utilizan para comunicarse entre sí. Las hormigas depositan feromonas en los caminos que recorren, y la cantidad de feromona en un camino influye en la probabilidad de que otras hormigas elijan ese camino. Con el tiempo, los caminos con mayores cantidades de feromona se vuelven más atractivos para las hormigas, lo que resulta en la aparición de una solución al problema de optimización.
El problema de ACO implica encontrar la solución óptima para un problema dado mediante la simulación del comportamiento de las hormigas. Típicamente consta de los siguientes pasos:
- Inicialización: Crear un conjunto de hormigas e inicializar los senderos de feromonas en todos los caminos.
- Movimiento de las hormigas: Cada hormiga selecciona probabilísticamente un camino basado en los niveles de feromona y la información heurística.
- Actualización de feromonas: Después de que todas las hormigas completen sus movimientos, se actualizan los niveles de feromona en los caminos según la calidad de las soluciones encontradas.
- Iteración: Repetir los pasos 2 y 3 durante un cierto número de iteraciones o hasta que se cumpla un criterio de terminación.
- Extracción de la solución: Se extrae la mejor solución encontrada por las hormigas.
Problema
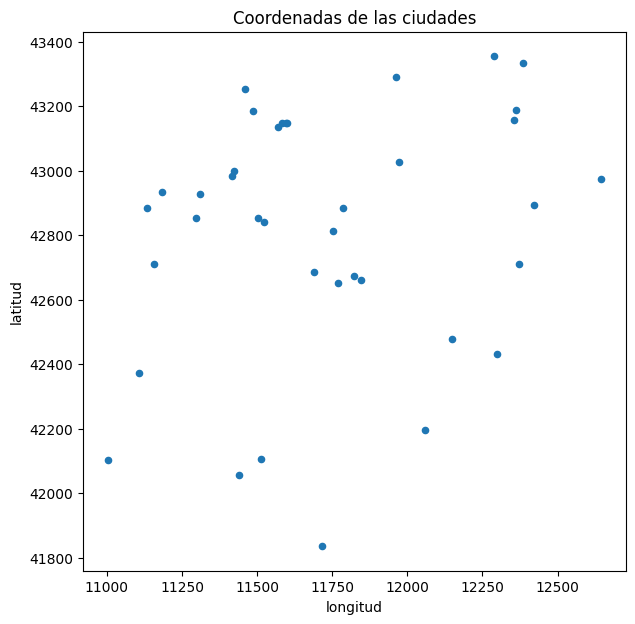
En nuestra simulación, nos centraremos en resolver el problema del Viajante en Djibouti, que consiste en encontrar el camino más corto que conecte \(38\) ciudades en Djibouti y regrese al punto de partida. Utilizaremos los datos proporcionados por la Universidad de Waterloo, donde se expone las coordenadas de las ciudades (ubicadas en el archivo data/dj38.tsp) y el camino óptimo (con una longitud de \(6656\) km). A lo largo de esta sección se utilizarán las librerias Pandas, Matplotlib y Numpy.
1
2
3
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
Visualización del problema
A continuación se mostrara un gráfico donde el eje-x representa la longitud y el eje-y representa la latitud. Cada punto del gráfico representa una ciudad por la cual se debera viajar.
1
2
3
df = pd.read_table("data/dj38.tsp", sep=" ")
df.plot.scatter(x="longitud", y="latitud", title="Coordenadas de las ciudades", figsize=(7, 7))
plt.show()
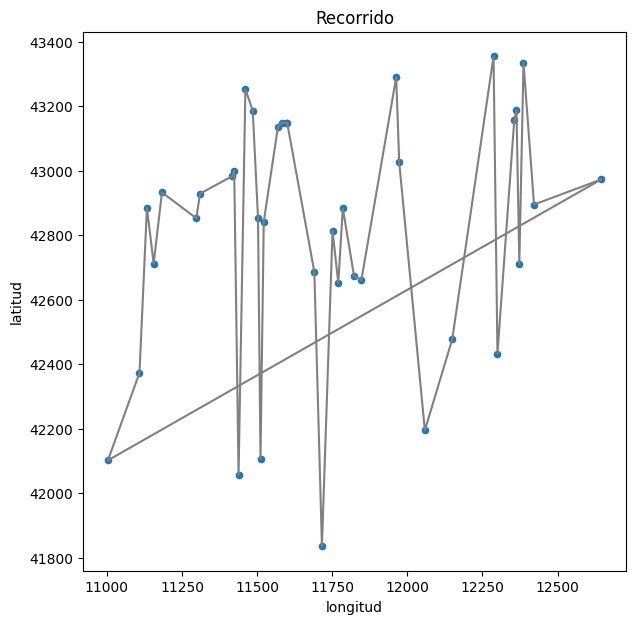
Definamos ahora la función show_path() que añada en el gráfico de las ciudades el recorrido especificado. Dicha función recibirá dos parámetros: df, que es el DataFrame que contiene las ciudades con sus coordenadas, y path, el cual es una lista de enteros indicando el índice de las ciudades a recorrer.
1
2
3
4
5
6
7
8
9
10
11
def show_path(df: pd.DataFrame, path: list[int]):
df = df.copy()
df["order"] = np.arange(len(df))
df = df.iloc[path]
# Plot cities
df.plot.scatter(x="longitud", y="latitud", title="Recorrido", figsize=(7, 7))
# Plot path
plt.plot(df["longitud"], df["latitud"], color="grey")
# Join last and first point
plt.plot([df.iloc[-1]["longitud"], df.iloc[0]["longitud"]], [df.iloc[-1]["latitud"], df.iloc[0]["latitud"]], color="grey")
plt.show()
Probemos graficar el recorrido que pasa por cada ciudad en orden, es decir, el recorrido que comienza por la ciudad 0, luego va a la ciudad 1, luego a la ciudad 2, y asi sucesivamente hasta llegar a la ciudad 37 y volver a la ciudad 0.
1
show_path(df, [i for i in range(len(df))])
Implementación de la colonia de hormigas
Se implementó la clase AntSystem, la cual permite simular la colonia de hormigas mediante el método run(), el cual recibe como parámetros max_cycles que es la cantidad de ciclos (o recorridos) y verbose que, en caso de ser verdadero, muestra en cada ciclo cual es la mejor solución encontrada. Además, la simulación puede ser completamente configurada mediante los atributos de la clase:
cities_distance: Una matriz cuadrada \(M_{2\times2}\) que contiene la distancia entre cada ciudad. La distancia entra la ciudad \(i\) y la ciudad \(j\) está representada por el elemento \(M_{ij}\)alpha: Factor de importancia de feromonas.beta: Factor de importancia heurística.evaporation_rate: Tasa de evaporación de las feromonas.n_ants: Número de hormigas.round_trip: Indica si las hormigas deben regresar a la ciudad de inicio.random_variable: Variable aleatoria discreta utilizada para la selección de ciudades.
Como se mencionó anteriormente, nos centraremos en comparar como cambia la solución encontrada por el algoritmo al configurar distintas variables aleatorias discretas.
Comenzaremos por obtener la matriz de distancia \(M\) a partir de los datos del problema. Para ello definimos la función distance() que calcula la distancia entre dos ciudades y la función distance_matrix() que calcula la matriz de distancias para un arreglo de ciudades determinado.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def distance(city1: tuple[int, int], city2: tuple[int, int]):
"""Calcula la distancia entre dos ciudades"""
return np.sqrt((city1[0] - city2[0]) ** 2 + (city1[1] - city2[1]) ** 2)
def distance_matrix(cities: np.ndarray):
"""Calcula la matriz de distancias"""
n_cities = len(cities)
cities_distance = np.zeros((n_cities, n_cities))
for i in range(n_cities):
for j in range(n_cities):
cities_distance[i, j] = distance(cities[i], cities[j])
return cities_distance
M = distance_matrix(df.values)
M
1
2
3
4
5
6
7
8
9
10
11
12
13
array([[ 0. , 290.99301545, 794.00183127, ..., 1852.35373049,
1624.75194088, 1858.09261272],
[ 290.99301545, 0. , 512.54097969, ..., 1598.94551098,
1412.88752368, 1649.18902517],
[ 794.00183127, 512.54097969, 0. , ..., 1331.29480435,
1288.37008374, 1514.19696932],
...,
[1852.35373049, 1598.94551098, 1331.29480435, ..., 0. ,
440.55907953, 444.22745405],
[1624.75194088, 1412.88752368, 1288.37008374, ..., 440.55907953,
0. , 236.48918264],
[1858.09261272, 1649.18902517, 1514.19696932, ..., 444.22745405,
236.48918264, 0. ]])
Por ejemplo, la distancia entre la ciudad 3 y la ciudad 4 es \(M_{3,4} \approx 222.539\) km, tal como se muestra a continuación.
1
M[3, 4]
1
222.53897723520097
Ahora, iniciaremos un sistema de hormigas con un factor de importancia de fermomonas \(\alpha=1\), un factor de importance heurística de \(\beta=5\) y una tasa de evaporación \(p = 0.5\), tal como se sugiere en [ACO]. Además el sistema estará compuesto de \(10\) hormigas y configuraremos un recorrido cerrado. A contiuación se muestra la función get_ant_system(), que recibe un generador de variables aleatorias discretas y retorna un sistema de hormigas con las características anteriormente descriptas.
1
2
3
4
5
6
7
8
9
10
11
12
13
from src.ant_system import AntSystem
from src.random_variable import DiscreteRandomVariable
def get_ant_system(discrete_random_variable: DiscreteRandomVariable):
return AntSystem(
cities_distance=M,
alpha=1,
beta=5,
n_ants=10,
round_trip=True,
evaporation_rate=0.5,
random_variable=discrete_random_variable,
)
Análisis de distintos generadores de números aleatorios
A continuación analizaremos como el rendimiento de distintos generadores de números aleatorios afecta al resultado obtenido por la simulación. Para ello definiremos tres generadores, los cuales serán sometidos a las distintas pruebas de aletoriedad, y luego se mostrarán los resultados obtenidos al ejecutar \(100\) ciclos de la simulación utilizando una variable aleatoria discreta compuesta por cada uno de los generadores.
1
2
from src import random_number
from src import randomness_test
Generador 1
El primero es un generador congruencial mixto, con una longitud de ciclo de \(43901\).
\(x_{n} = \left( 127x_{n-1} + 52711 \right)\bmod 87803\) \(x_0 = 111\)
1
2
generator1 = random_number.MixedCongruentialGenerator(a=127, b=52711, m=87803, seed=111)
print(len(generator1))
1
43901
Pruebas de aletoriedad
A continuación se realiza la prueba de Chi Cuadrada con \(11\) intervalos y un nivel de significancia de \(\alpha = 0.01\). El valor del estadístico es \(\chi^2_{(v=10, \alpha=0.01)} = 23.2093\)
1
randomness_test.ChiSquaredTest(generator1.get_random_numbers(), intervals=11, statistic=23.2093).run_test()
Ahora, realizamos la prueba de Kolmogorov-Smirnov con un nivel de significancia de \(\alpha = 0.01\). El valor del estadístico es \(D(\alpha, n) = \frac{1.63}{43901}\)
1
randomness_test.KolmogorovSmirnovTest(generator1.get_random_numbers(), statistic=1.63/len(generator1)).run_test()
Debido a la extensa longitud de la secuencia de números aleatorios generadas, se realiza la prueba de Rachas para los primeros \(100\) números aleatorios generados, con un nivel de significancia de \(\alpha = 0.0099\). El valor del estadístico es \(Z = 2.33\)
1
randomness_test.WaldWolfowitzRunsTest(generator1.get_random_numbers()[:100], statistic=2.33).run_test()
Rachas: [0.00126419] [0.76088516] [0.23274831 0.15936813] … [0.41868729] [0.77361821]
\(b = 54\) (cantidad de rachas)
\(n_1 = 56\) (cantidad de números positivos)
\(n_2 = 44\) (cantidad de números negativos)
\(Z_{\alpha/2}\) = 2.33
\[Z_0 = \frac{b - \mu_b}{\sigma_b} = 0.8608174614728519\]-\(Z_{\alpha/2}\) \(\leq Z_0 \leq\) \(Z_{\alpha/2}\) \(\Rightarrow\) La hipótesis se acepta.
Resultado de la simulación
Una vez realizadas las pruebas de aletoriedad, pasamos a crear la variable aleatoria discreta y ejecutar la simulación.
1
2
3
4
5
6
7
8
generator1.reset()
ant_system1 = get_ant_system(
DiscreteRandomVariable(generator1, values=None, weights=None)
)
ant_system1.run(max_cycles=100)
print(f"Mejor recorrido encontrado: {ant_system1.best_solution}", end="\n\n")
print(f"Longitud del mejor recorrido: {ant_system1.best_solution_cost}")
1
2
3
4
Mejor recorrido encontrado: [11 10 8 7 6 5 4 2 3 1 0 9 13 20 28 29 31 34 36 37 32 33 35 30
26 27 23 21 25 24 22 19 14 12 18 17 16 15]
Longitud del mejor recorrido: 6667.029907787184
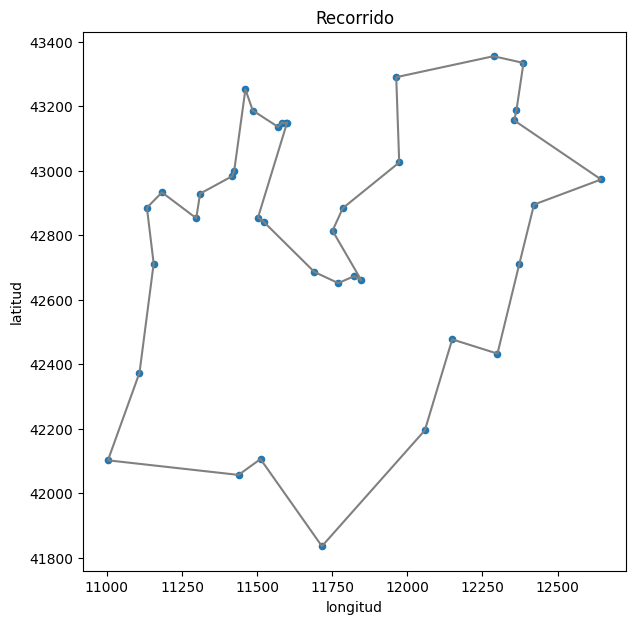
Podemos visualizar el mejor recorrido encontrado en el siguiente gráfico.
1
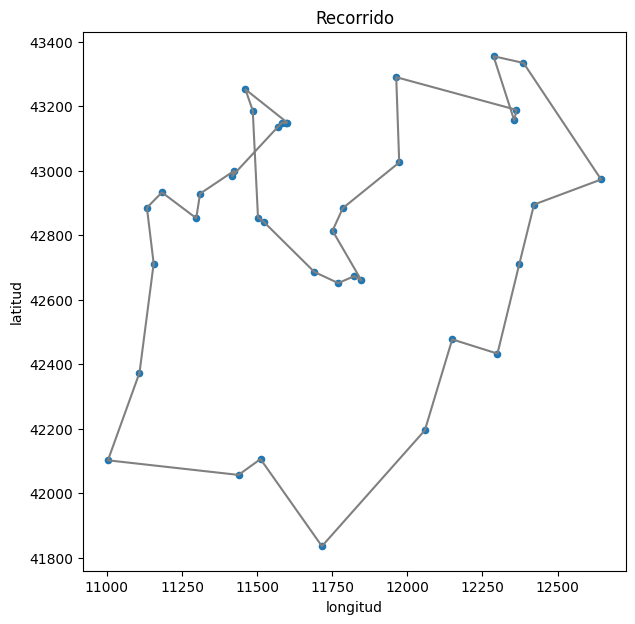
show_path(df, ant_system1.best_solution)
Como se puede observar, el Generador 1 pasó la prueba de la Chi Cuadrada y de Rachas, sin embargo no pasó la prueba de Kolmogorov-Smirnov. El mejor recorrido encontrado utilizando este generador tiene una longitud de aproximadamente \(6667.03\) kilómetros, tan solo \(11.03\) kilómetros por arriba del óptimo.
Generador 2
El segundo es un generador congruencial mixto de ciclo completo, con una longitud de ciclo de \(128\).
\(x_{n} = \left( 5 x_{n-1} + 7 \right)\bmod 128\) \(x_0 = 4\)
1
2
generator2 = random_number.MixedCongruentialGenerator(a=5, b=7, m=128, seed=4)
print(len(generator2))
1
128
Pruebas de aletoriedad
A continuación se realiza la prueba de Chi Cuadrada con \(11\) intervalos y un nivel de significancia de \(\alpha = 0.01\). El valor del estadístico es \(\chi^2_{(v=10, \alpha=0.01)} = 23.2093\)
1
randomness_test.ChiSquaredTest(generator2.get_random_numbers(), intervals=11, statistic=23.2093).run_test()
Ahora, realizamos la prueba de Kolmogorov-Smirnov con un nivel de significancia de \(\alpha = 0.01\). El valor del estadístico es \(D(\alpha, n) = \frac{1.63}{128}\)
1
randomness_test.KolmogorovSmirnovTest(generator2.get_random_numbers(), statistic=1.63/len(generator2)).run_test()
Por último, se realiza la prueba de Rachas con un nivel de significancia de \(\alpha = 0.0099\). El valor del estadístico es \(Z = 2.33\).
1
randomness_test.WaldWolfowitzRunsTest(generator2.get_random_numbers(), statistic=2.33).run_test()
Rachas: [0.03125 0.2109375 0.109375 ] [0.6015625] [0.0625 0.3671875] … [0.5 0.5546875 0.828125 ] [0.1953125]
\(b = 55\) (cantidad de rachas)
\(n_1 = 64\) (cantidad de números positivos)
\(n_2 = 64\) (cantidad de números negativos)
\(Z_{\alpha/2}\) = 2.33
\[Z_0 = \frac{b - \mu_b}{\sigma_b} = -1.6860296357240232\]-\(Z_{\alpha/2}\) \(\leq Z_0 \leq\) \(Z_{\alpha/2}\) \(\Rightarrow\) La hipótesis se acepta.
Resultado de la simulación
Finalizadas las pruebas de aletoriedad, creamos la variable aleatoria discreta y ejecutamos la simulación.
1
2
3
4
5
6
7
8
9
generator2.reset()
ant_system2 = get_ant_system(
DiscreteRandomVariable(generator2, values=None, weights=None)
)
ant_system2.random_variable = DiscreteRandomVariable(generator2, values=None, weights=None)
ant_system2.run(max_cycles=100)
print(f"Mejor recorrido encontrado: {ant_system2.best_solution}", end="\n\n")
print(f"Longitud del mejor recorrido: {ant_system2.best_solution_cost}")
1
2
3
4
Mejor recorrido encontrado: [ 1 0 9 13 20 28 29 31 34 36 37 35 30 32 33 26 27 23 21 25 24 22 19 14
12 11 10 18 17 16 15 7 8 6 5 4 2 3]
Longitud del mejor recorrido: 6987.756667236131
Podemos visualizar el mejor recorrido encontrado en el siguiente gráfico.
1
show_path(df, ant_system2.best_solution)
Como se puede observar, el Generador 2 pasó todas las pruebas de aletoriedad. El mejor recorrido encontrado utilizando este generador tiene una longitud de aproximadamente \(6987.76\) kilómetros, con \(331.76\) kilómetros por arriba del óptimo.
El Generador 2, a diferencia del Generador 1, superó el prueba de Kolmogorov-Smirnov, lo que sugiere que presenta una mayor uniformidad y por ende, es un mejor generador. Sin embargo el Generador 1 logró mejores resultados. Esto puede justificarse debido que la longitud del Generador 2 es minúscula, tan solo puede generar \(128\) números aleatorios diferentes, mientras que el Generador 1 consigue una secuencia de \(43901\) números aleatorios distintos.
Generador 3
El tercer es un generador dependiente, con una longitud de ciclo de \(2^{20}\).
\(x_n = \begin{cases} x_{n-1} - 1 &\quad\text{si } x_{n-1} > 0\\ x_0 &\quad\text{si } x_{n-1} = 0\\ \end{cases}\) \(x_0 = 2^{20} - 1\)
1
2
generator3 = random_number.DependentGenerator(seed=2**20 - 1)
len(generator3)
1
1048576
Pruebas de aletoriedad
A continuación se realiza la prueba de Chi Cuadrada con \(11\) intervalos y un nivel de significancia de \(\alpha = 0.01\). El valor del estadístico es \(\chi^2_{(v=10, \alpha=0.01)} = 23.2093\)
1
randomness_test.ChiSquaredTest(generator3.get_random_numbers(), intervals=11, statistic=23.2093).run_test()
Ahora, realizamos la prueba de Kolmogorov-Smirnov con un nivel de significancia de \(\alpha = 0.01\). El valor del estadístico es \(D(\alpha, n) = \frac{1.63}{1048576}\)
1
randomness_test.KolmogorovSmirnovTest(generator3.get_random_numbers(), statistic=1.63/len(generator3)).run_test()
Debido a la extensa longitud de la secuencia de números aleatorios generadas, se realiza la prueba de Rachas para los primeros \(100\) números aleatorios generados, con un nivel de significancia de \(\alpha = 0.0099\). El valor del estadístico es \(Z = 2.33\)
1
randomness_test.WaldWolfowitzRunsTest(generator3.get_random_numbers()[:100], statistic=2.33).run_test()
Rachas: [1. 0.99999905 …] [0.99995232 0.99995136 …]
\(b = 2\) (cantidad de rachas)
\(n_1 = 50\) (cantidad de números positivos)
\(n_2 = 50\) (cantidad de números negativos)
\(Z_{\alpha/2}\) = 2.33
\[Z_0 = \frac{b - \mu_b}{\sigma_b} = -9.74936418649013\]\(Z_0 <\) -\(Z_{\alpha/2}\) \(\Rightarrow\) La hipótesis se rechaza.
Resultado de la simulación
Finalizadas las pruebas de aletoriedad, continuamos con la creación de la variable aleatoria discreta y la ejecución la simulación.
1
2
3
4
5
6
7
8
9
generator3.reset()
ant_system3 = get_ant_system(
DiscreteRandomVariable(generator3, values=None, weights=None)
)
ant_system3.random_variable = DiscreteRandomVariable(generator3, values=None, weights=None)
ant_system3.run(max_cycles=100)
print(f"Mejor recorrido encontrado: {ant_system3.best_solution}", end="\n\n")
print(f"Longitud del mejor recorrido: {ant_system3.best_solution_cost}")
1
2
3
4
Mejor recorrido encontrado: [37 36 35 33 32 34 31 29 28 27 30 26 25 24 22 23 21 19 18 17 16 15 14 12
11 10 8 7 6 5 4 2 3 20 13 9 1 0]
Longitud del mejor recorrido: 11000.700585251023
Podemos visualizar el mejor recorrido encontrado en el siguiente gráfico.
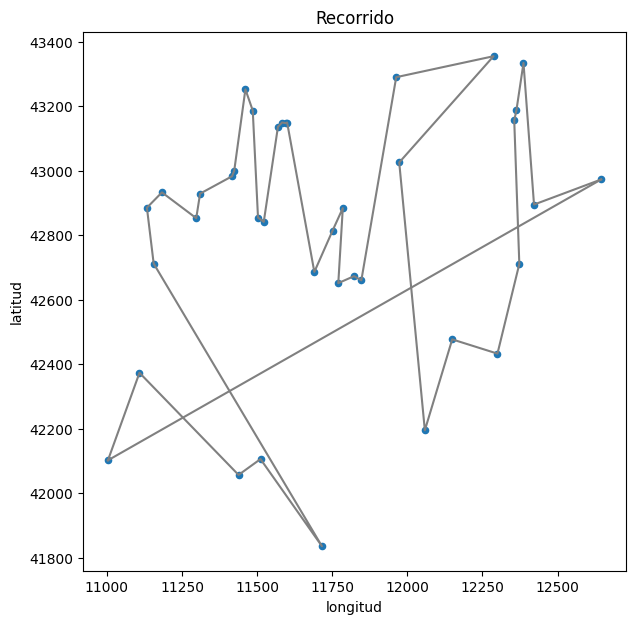
1
show_path(df, ant_system3.best_solution)
Como era de esperarse, el Generador 3 pasa las pruebas de uniformidad pero no de independencia, y es justamente la fuerte dependencia en la generación de los números aleatorios la que provoca que la simulación devuelva pésimos resultados. Como se muestra anteriormente, el mejor viaje encontrado tiene una longitud de \(11000.70\) kilómetros, \(4344.70\) kilómetros más que la solución óptima.
Conclusión
A lo largo de nuestros experimentos, hemos llevado a cabo un exhaustivo análisis sobre cómo los generadores de números aleatorios afectan la construcción y el desempeño de simulaciones. Hemos observado que diversos factores, como la longitud de la secuencia generada, la uniformidad y la independencia de los números aleatorios, desempeñan un papel crucial en la calidad y la confiabilidad de las simulaciones.
Nuestros resultados destacan la relevancia de seleccionar cuidadosamente un generador de números aleatorios apropiado para cada simulación. Encontramos que los generadores de alta calidad, con secuencias más largas y una mayor uniformidad, son fundamentales para reducir el sesgo y mejorar la precisión de los resultados obtenidos. Estos generadores generan secuencias que se asemejan más a la distribución deseada, lo que favorece la representación realista de los fenómenos modelados.
La independencia de los números aleatorios también es un aspecto crítico. Generadores que producen números aleatorios independientes garantizan que cada valor generado sea verdaderamente independiente de los anteriores, evitando cualquier influencia no deseada entre las variables simuladas. Esto es esencial para obtener resultados fiables y evitar sesgos en la simulación.
Además, durante nuestros experimentos, hemos observado que el rendimiento de la simulación puede verse afectado por la elección del generador de números aleatorios. Generadores con ciclos más amplios y mayor capacidad para generar números verosímiles permiten explorar un espacio de soluciones más completo y obtener resultados más precisos en menos iteraciones.
En resumen, la elección adecuada del generador de números aleatorios es un factor crítico en la construcción de simulaciones confiables y precisas. Los generadores de alta calidad, con secuencias largas, uniformidad y independencia, son fundamentales para reducir el sesgo y mejorar la representación de fenómenos complejos. Asimismo, la selección de generadores con ciclos suficientemente amplios permite obtener resultados más rápidos y precisos. Estos hallazgos son de vital importancia para la comunidad de simulación, ya que contribuyen a mejorar la confiabilidad y la validez de los resultados obtenidos en diversos campos de estudio.
Bibliografía
- [ACO] Ant System: Optimization by a colony of cooperating agents. IEEE Trans Syst Man Cybernetics - Part B. Marco Doringo, Alberto Colorni, Vittorio Maniezzo.