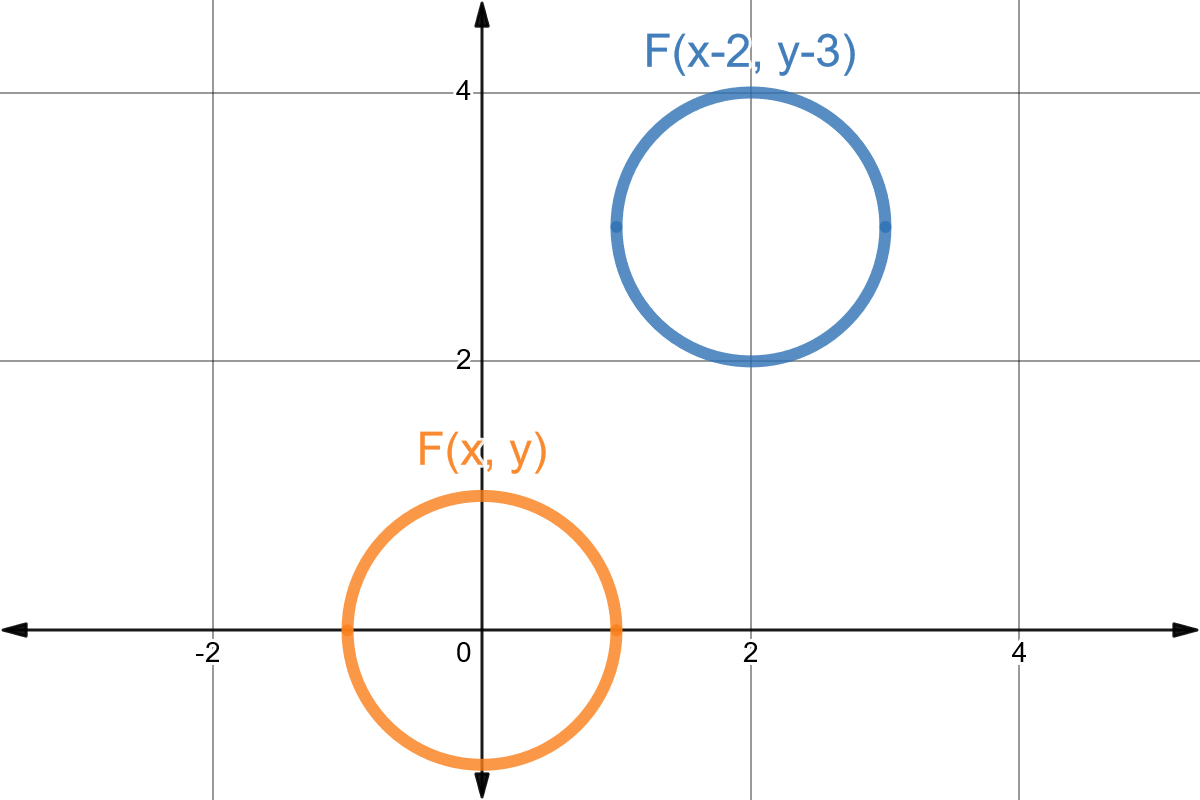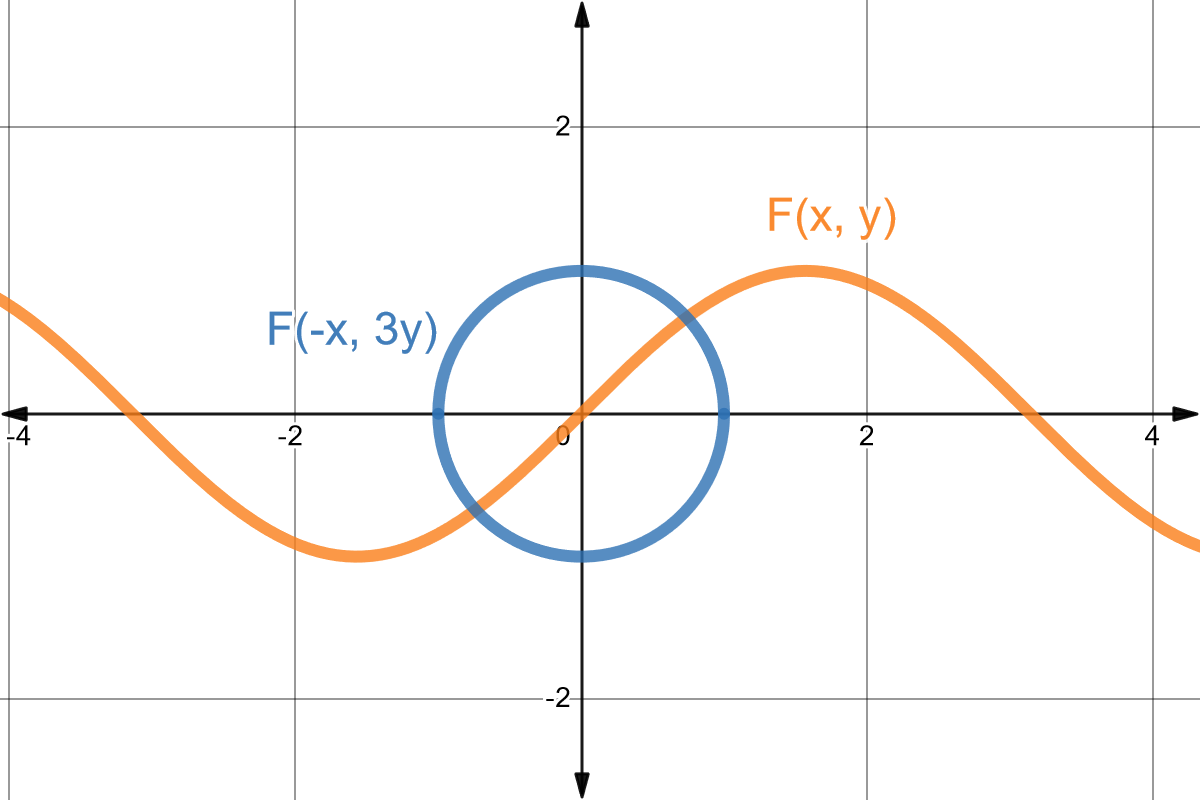Descubriendo la Belleza de las Ecuaciones Implícitas
¡Queridos lectores y amantes de las matemáticas! Hoy estoy emocionado de compartir con ustedes mi participación en un concurso muy especial organizado por Mates Mike, un creador de contenidos que enseña matemáticas mediante animaciones. El desafío consiste en encontrar una ecuación implícita \(F(x, y) = 0\) con un gráfico sorprendente. Considero esta oportunidad perfecta para explorar y compartir el fascinante mundo de las gráficas generadas por ecuaciones implícitas y funciones implícitas.
En este artículo, les llevaré en un viaje de descubrimiento, donde exploraremos diversas técnicas y propiedades para crear gráficas fascinantes mediante ecuaciones implícitas. A medida que avanzamos, desvelaré los secretos y conceptos que he aprendido a lo largo del concurso. ¡Espero que encuentren inspiración y disfruten de esta experiencia tanto como yo!
Introducción a las ecuaciones y funciones implícitas
¿Qué es una ecuación implícita?
Una ecuación implícita es una relación de la forma \(F(x_1, \dots, x_n) = 0\) donde \(F\) es una función de las variables \(x_1, \dots, x_n\). Por otro lado, se denomina lugar geométrico al conjunto de puntos \(P(x_1, \dots, x_n)\) de \(\mathbb{R}^n\) que verifican la ecuación implícita \(F\).
El lugar geométrico de una ecuación implícita es simplemente la gráfica de la misma.
Por ejemplo pensemos en la ecuación implícita de dos variables
\[F(x, y) = x^2 - 4xy = 0\]¿Qué tipo de lugar geométrico representa? Dicho de otro modo, ¿qué curva determinan los puntos que verifican esta ecuación? Si sacamos factor común \(x\) obtenemos:
\[x(x-4y) = 0\]Por lo tanto, los puntos que verifican la ecuación implícita \(F(x, y) = 0\) son los puntos de la recta \(x = 0\) y los puntos de la recta \(x = 4y\).
Podemos graficar este lugar geométrico en Desmos:
¿Qué es una función implícita?
Una función implícita es una función que se define mediante una ecuación implícita, y relaciona una de las variables, llamada variable dependiente, con las demás variables, llamadas variables independientes.
\[F(x, y) = 0 \iff y = f(x)\]La principal diferencia entre una ecuación implícita y una función implícita es que la ecuación implícita no diferencia entre variables independientes y dependientes, mientras que la función implícita sí. Podemos decir que toda función implícita es una ecuación implícita, mientras que no toda ecuación implícita es una función implícita.
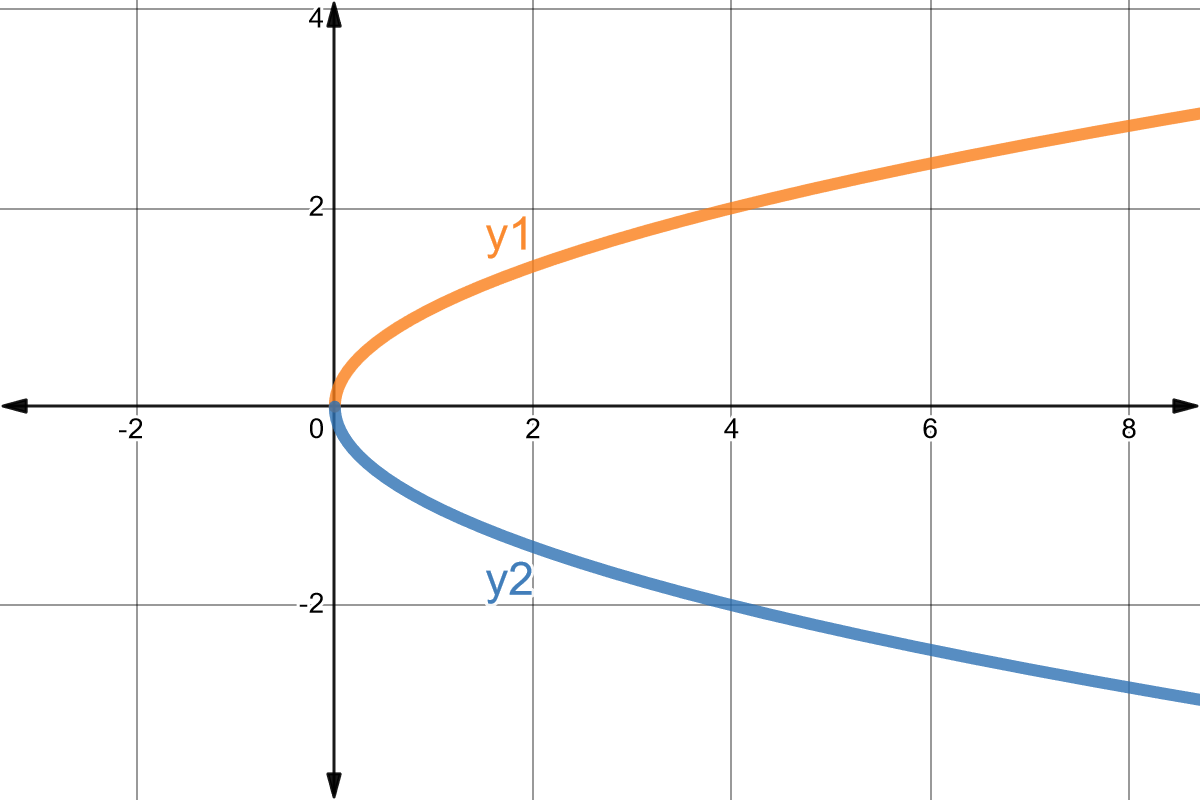
En general, una ecuación implícita tiene múltiples funciones implícitas si, al resolver para \(y\), llegamos a un paso en el que tenemos que tomar una decisión, como una raíz cuadrada. Por ejemplo, consideremos la ecuación implícita \(y^2 - x = 0\). Al resolver para \(y\) obtenemos:
\[y^2 = x\] \[y = \pm \sqrt{x}\]Por lo tanto, esta ecuación implícita está definida por dos funciones implícitas:
\[y_1 = \sqrt{x} \quad \land \quad y_2 = -\sqrt{x}\]Ecuación implícita de la circunferencia
Una circunferencia es el lugar geométrico conformado por el conjunto de todos los puntos de un plano que equidistan de un punto fijo \(C\) llamado centro. La distancia desde cualquier punto \(P\) de la circunferencia al centro \(C\), se denomina radio y se denota por \(r\).
Sea \(P(x, y)\) un punto cualquiera de la circunferencia que tiene centro \(C(a, b)\) y cuyo radio mide \(r\). Entonces por la definición de circunferencia \(d(P, C)=r\), es decir, la distancia euclidiana entre el centro de la circunferencia y un punto cualquiera de la misma es igual al radio.
\[d(P, C) = r \iff \sqrt{(x - a)^2 + (y - b)^2} = r\]De allí se deduce que:
\[(x - a)^2 + (y - b)^2 = r^2\]Esta es la ecuación implícita de la circunferencia de radio \(r\) y centro \((a, b)\), y el lugar geométrico de la circunferencia es:
\[\{(x, y) \in \mathbb{R}^2 \mid (x - a)^2 + (y - b)^2 = r^2\}\]Tomemos el ejemplo de una circunferencia con centro en el origen y radio \(r = 1\). La ecuación implícita de esta circunferencia es:
\[x^2 + y^2 = 1\]Su lugar geométrico es:
Propiedades de las ecuaciones implícitas
A continuación veremos varias propiedades de las ecuaciones implícitas con las que podremos trasladar, expandir, comprimir, reflejar y combinar distintos lugares geométricos. De esta manera podremos transformar las gráficas que deseemos para crear nuevas gráficas sorprendentes con suma facilidad.
Traslación
Con esta propiedad podremos desplazar nuestras gráficas a lo largo del plano. Dada una ecuación implícita \(F(x, y) = 0\), el lugar geométrico de \(F\) trasladado \(a\) unidades en el eje \(x\) y \(b\) unidades en el eje \(y\) está definido por la ecuación implícita:
\[F(x - a, y - b) = 0\]Demostración
Podemos demostrar la traslación fácilmente al considerar las variables de sustitución \(u = x-a\) y \(v = y-b\), de tal modo que \(F(x-a, y-b) = F(u, v)\). Sea \(P(u, v) = (x_0, y_0)\) un punto cualquiera que pertenezca al lugar geométrico de \(F(u, v) = 0\), podemos observar que:
\[\begin{align*} P(u, v) &= (x_0, y_0) \\ P(x-a, y-b) &= (x_0, y_0) \\ P((x-a) + a, (y-b) + b) &= (x_0 + a, y_0 + b) \\ \therefore P(x, y) &= (x_0 + a, y_0 + b) \end{align*}\]Ejemplo
Como ejemplo consideremos un círculo unitario de radio \(1\) centrado en el origen. Su ecuación implícita es \(F(x, y) = x^2 + y^2 - 1 = 0\). Si trasladamos el círculo \(2\) unidades en el eje \(x\) y \(3\) unidades en el eje \(y\), la ecuación implícita del círculo trasladado es:
\[F(x-2, y-3) = (x-2)^2 + (y-3)^2 - 1 = 0\]Y su lugar geométrico es:
Expansión, compresión y reflexión
Con la siguiente propiedad podremos estirar, achicar e invertir el sentido de nuestras gráficas con respecto a los distintos ejes. Sea \(F(x, y) = 0\), la ecuación implícita de la misma curva pero expandida, comprimida y/o reflejada en \(a\) unidades en el eje \(x\) y \(b\) unidades en el eje \(y\) es:
\[F(a x, b y) = 0\]Donde si:
- \(0 < \|a\| < 1\): expansión con respecto al eje \(x\).
- \(\|a\| > 1\): contracción con respecto al eje \(x\).
- \(a < 0\): reflexión con respecto al eje \(y\).
- \(0 < \|b\| < 1\): expansión con respecto al eje \(y\).
- \(\|b\| > 1\): contracción con respecto al eje \(y\).
- \(b < 0\): reflexión con respecto al eje \(x\).
Notemos que un valor negativo de \(a\) produce una reflexión sobre el eje \(y\) y no sobre el eje \(x\), asi como también un valor negativo de \(b\) produce una reflexión sobre el eje \(x\).
Demostración
Para demostrar esto realizaremos el mismo procedimiento que para demostrar la propiedad de traslación. Definimos las variables de sustitución \(u = a x\) y \(v = b y\), por lo que \(F(a x, b y) = F(u, v)\), y un punto cualquiera \(P(u, v) = (x_0, y_0)\) que pertenezca al lugar geométrico de \(F(u, v) = 0\):
\[\begin{align*} P(u, v) &= (x_0, y_0) \\ P(a x, b y) &= (x_0, y_0) \\ P(\frac{a x}{a}, \frac{b y}{b}) &= (\frac{x_0}{a}, \frac{y_0}{b}) \\ \therefore P(x, y) &= (\frac{x_0}{a}, \frac{y_0}{b}) \end{align*}\]Ejemplo
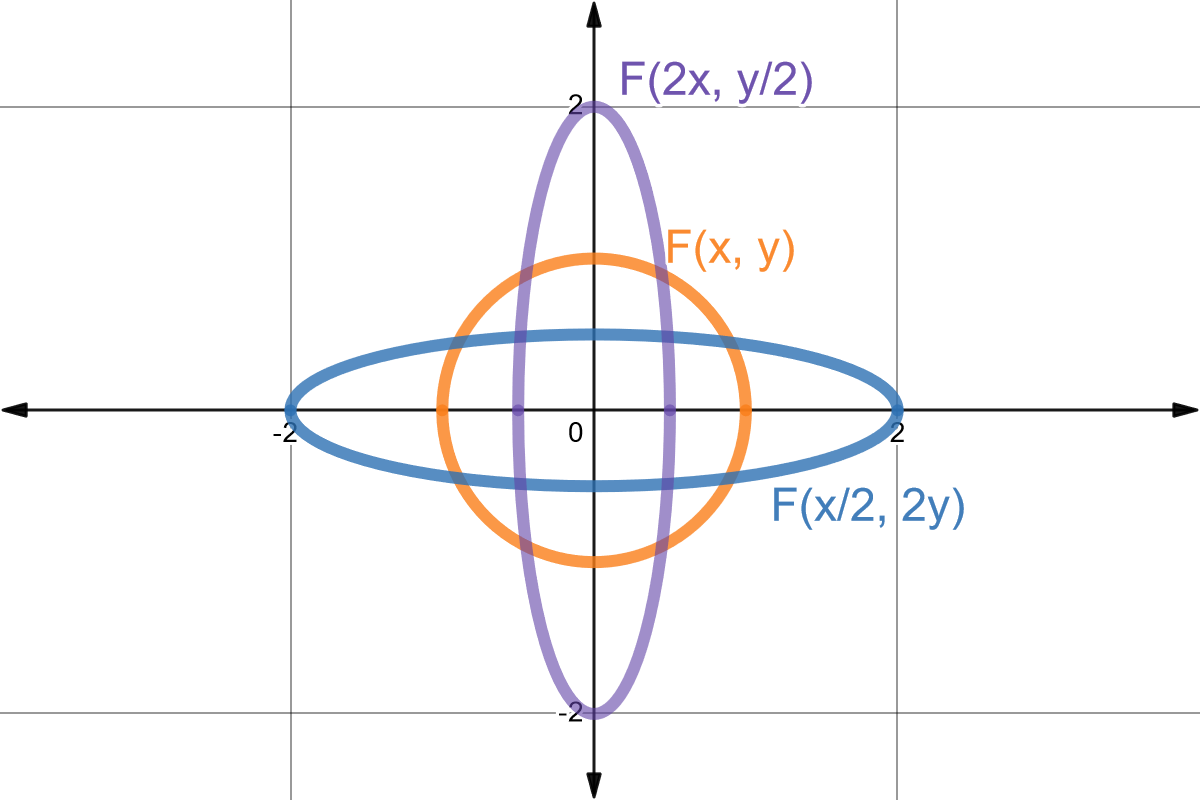
Dada la ecuación implícita del círculo unitario \(F(x, y) = x^2 + y^2 - 1 = 0\), podemos encontrar la circunferencia expandida al doble con respecto al eje \(x\) y comprimida a la mitad con respecto al eje \(y\), \(F(\frac{1}{2}x, 2y)\); y la circunferencia comprimida a la mitad con respecto al eje \(x\) y expandida al doble con respecto al eje \(y\), \(F(2x, \frac{1}{2}y)\).
Ahora tomemos la ecuación implícita de la parábola \(G(x, y) = y^2 - x = 0\) y observemos como la ecuación implícita \(G(-x, 3y)=0\) es la misma parábola, pero reflejada sobre el eje \(y\) y comprimida al triple sobre ese mismo eje.
Unión
Esta propiedad nos permite unir varias gráficas en una gráfica más grande. Esto es muy interesante en el caso que queramos juntar dos lugares geométricos que deseemos. Dada dos ecuaciones implícitas \(F(x, y)=0\) y \(G(x, y)=0\), la ecuación implícita cuyo lugar geométrico es la unión de los lugares geométricos de \(F\) y \(G\) es:
\[F(x, y) \cdot G(x, y) = 0\]Demostración
Para demostrar la propiedad de la unión, sencillamente notemos que:
\[F(x, y) \cdot G(x, y) = 0 \iff F(x, y) = 0 \lor G(x, y) = 0\]Por lo que el lugar geométrico \(D\) de \(F(x, y) \cdot G(x, y) = 0\) es:
\[\begin{align*} D &= \{(x, y) \in \mathbb{R}^2 \mid F(x, y) = 0\} \quad \cup \quad \{(x, y) \in \mathbb{R}^2 \mid G(x, y) = 0\} \\ \therefore D &= \{(x, y) \in \mathbb{R}^2 \mid F(x, y) = 0 \lor G(x, y) = 0\} \end{align*}\]Ejemplo
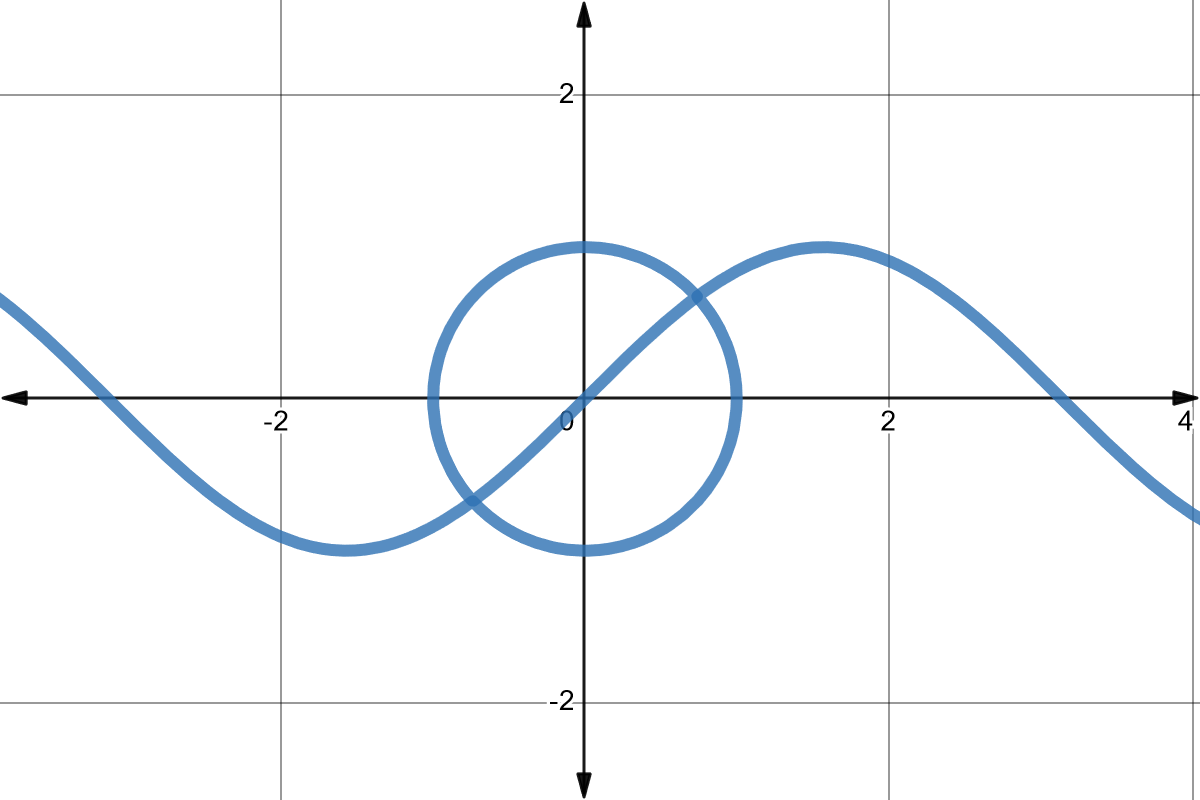
Tomemos el ejemplo de la función implícita del seno \(F(x, y) = y - \sin{x} = 0\) y la ecuación implícita del círculo unitario centrado en el origen \(G(x, y) = x^2 + y^2 - 1 = 0\).
Si aplicamos la propiedad de la union para \(F\) y \(G\) obtendremos la ecuación implícita:
\[F(x, y) \cdot G(x, y) = (y - \sin{x}) \cdot (x^2 + y^2 - 1) = 0\]Cuyo lugar geométrico es la combinación de los lugares geométricos de \(F\) y \(G\):
Reducción de los lugares geométricos
Llamamos reducción de los lugares geométricos a la técnica mediante la cual se eliminan algunos puntos del lugar geométrico de una ecuación implícita. Esto nos permite combinar lugares geométricos de diversas maneras, ampliando extensamente nuestro abanico de posibilidades para crear gráficas.
Definición
Dada una ecuación implícita \(F(x_1, \dots, x_n) = 0\) con lugar geométrico \(D_F\), definimos la ecuación geométrica reducida \(F'(x_1, \dots, x_n) = 0\) con lugar geométrico \(D_{F'}\), donde
\[D_{F'} \subseteq D_{F}\]y la función de reducción \(\Phi : \mathbb{R}^n - R \rightarrow \{1\}\) tal que
\[F'(x_1, \dots, x_n) = F(x_1, \dots, x_n) \cdot \Phi(x_1, \dots, x_n)\]donde \(R\) es el conjunto de reducción que contiene los puntos que buscamos eliminar del lugar geométrico de \(F(x_1, \dots, x_n) = 0\). De este modo, el lugar geométrico de \(F'(x_1, \dots, x_n) = 0\) que determinado como
\[D_{F'} = \{(x_1, \dots, x_n) \in \mathbb{R}^n \mid F(x_1, \dots, x_n) = 0 \land (x_1, \dots, x_n) \notin R\}\]Explicación
La idea es encontrar una manera de eliminar un conjunto de puntos \(R\) del lugar geométrico definido por la función implicita \(F(x_1, \dots, x_n) = 0\). Para ello buscamos una función de reducción \(\Phi\) que devuelva \(1\) para cualquier valor de \(x_1, x_2, \dots, x_n\), pero cuyo dominio este restringido por \(R\), de modo que \(F(x_1, \dots, x_n) \cdot \Phi = F(x_1, \dots, x_n)\) para todos los puntos de \(D_F\) a excepción de aquellos valores que se encuentren en \(R\). De esta manera, el lugar geométrico de la ecuación implícita reducida \(D_{F'}\) queda determinado por todos los puntos que pertenezcan a \(D_F\) menos aquellos que también pertenecen a \(R\), es decir:
\[D_{F'} = D_F - R\]Para lograr esto utilizamos ciertas indeterminaciones matemáticas como son la división por cero y la raíz cuadrada de números negativos, como se analizará mas a detalle en las siguientes secciones.
Reducción por distinción
Objetivo
La reducción por distinción permite eliminar los puntos de un lugar geométrico que también pertenecen a otro lugar geométrico. Es decir, teniendo las ecuaciones implícitas \(F(x_1, \dots, x_n) = 0\) y \(G(x_1, \dots, x_n) = 0\), buscamos eliminar del lugar geométrico de \(F\) aquellos puntos que también verifican la ecuación implícita de \(G\). El conjunto de reducción \(R\) es entonces:
\[R = D_F - D_G\]donde \(D_F\) es el lugar geométrico de \(F\) y \(D_G\) es el lugar geométrico de \(G\).
Función de reducción
Dadas las ecuaciones implícitas \(F(x_1, \dots, x_n) = 0\) y \(G(x_1, \dots, x_n) = 0\), definimos la función de reducción \(\Phi(x_1, \dots, x_n)\) como
\[\Phi(x_1, \dots, x_n) = \frac{G(x_1, \dots, x_n)}{G(x_1, \dots, x_n)}\]de modo que
\[F'(x_1, \dots, x_n) = F(x_1, \dots, x_n) \cdot \frac{G(x_1, \dots, x_n)}{G(x_1, \dots, x_n)}\]con lugar geométrico igual a
\[D_F' = \{(x_1, \dots, x_n) \in \mathbb{R}^n \mid F(x_1, \dots, x_n) = 0 \land G(x_1, \dots, x_n) \neq 0\}\]Reducción por desigualdad
Objetivo
Con la reducción por desigualdad buscamos eliminar los puntos de un lugar geométrico que verifiquen una determinada inecuación de menor o igual. Consideremos la ecuación implícita \(F(x_1, \dots, x_n) = 0\) y la inecuación \(G(x_1, \dots, x_n) \leq 0\), buscamos eliminar del lugar geométrico \(D_F\) aquellos puntos que verifiquen la inecuación. El conjunto de reducción \(R\) queda definido como:
\[R = D_F - \{(x_1, \dots, x_n) \in \mathbb{R}^n \mid G(x_1, \dots, x_n) \leq 0\}\]donde \(D_F\) es el lugar geométrico de \(F\).
Función de reducción
Dadas la ecuación implícita \(F(x_1, \dots, x_n) = 0\) y la inecuación \(G(x_1, \dots, x_n) \leq 0\), definimos la función de reducción \(\Phi(x_1, \dots, x_n)\) como
\[\Phi(x_1, \dots, x_n) = \frac{\sqrt{G(x_1, \dots, x_n)}}{\sqrt{G(x_1, \dots, x_n)}}\]de modo que
\[F'(x_1, \dots, x_n) = F(x_1, \dots, x_n) \cdot \frac{\sqrt{G(x_1, \dots, x_n)}}{\sqrt{G(x_1, \dots, x_n)}}\]con lugar geométrico igual a
\[D_F' = \{(x_1, \dots, x_n) \in \mathbb{R}^n \mid F(x_1, \dots, x_n) = 0 \land G(x_1, \dots, x_n) > 0\}\]Corolario de la reducción por desigualdad
Podemos eliminar los puntos de un lugar geométrico que verifiquen una determinada inecuación de mayor o igual. Para ello consideremos la ecuación implícita \(F(x_1, \dots, x_n) = 0\) y la inecuación \(M(x_1, \dots, x_n) \leq 0\) donde
\[M(x_1, \dots, x_n) = -G(x_1, \dots, x_n)\]De este modo obtenemos la inecuación \(M(x_1, \dots, x_n) \leq 0\), que es equivalente a la inecuación \(G(x_1, \dots, x_n) \geq 0\), y la función de reducción es
\[\Phi(x_1, \dots, x_n) = \frac{\sqrt{-G(x_1, \dots, x_n)}}{\sqrt{-G(x_1, \dots, x_n)}}\]Ejemplo
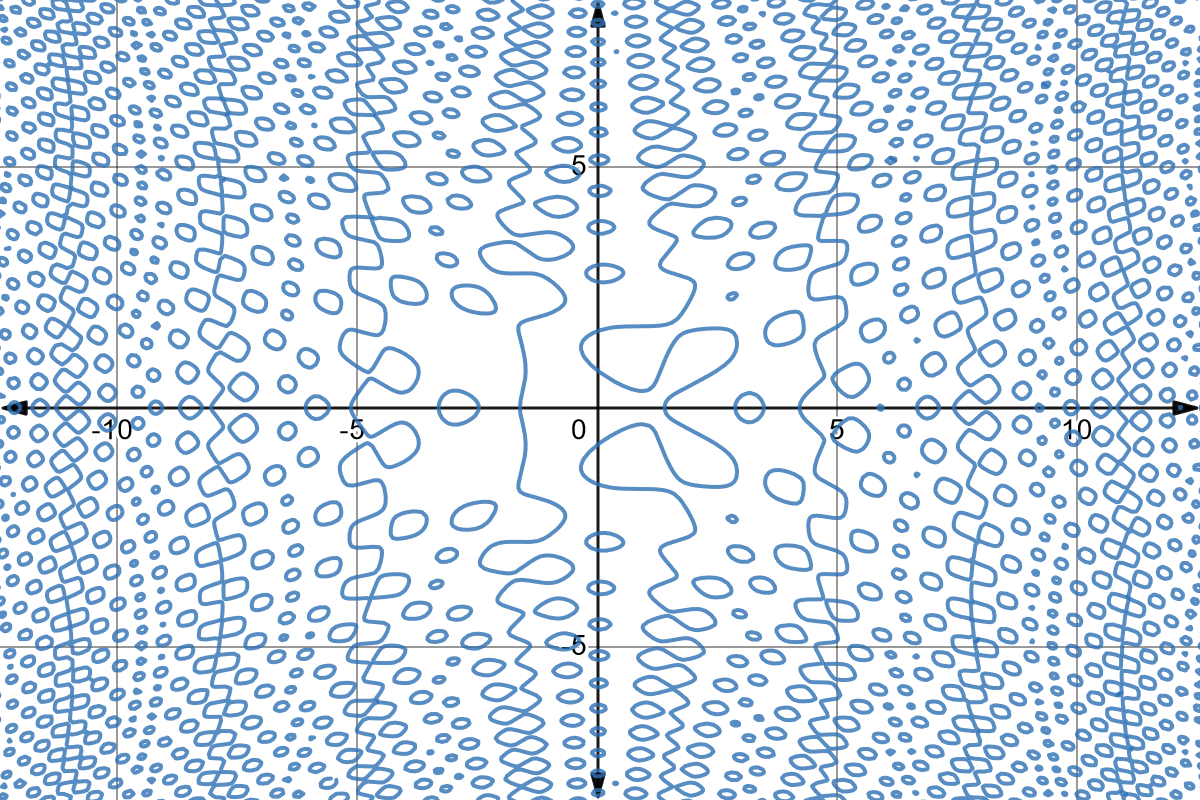
Consideremos la ecuación implícita \(F(x, y) = \cos\left(x+\cos\left(yx\right)-\sin\left(x^{2}-y^{2}\right)\right)=0\), que genera el increíble lugar geométrico:
y la inecuación del círculo de radio \(\sqrt{50}\) centrado en el origen, \(G(x,y)=x^{2}+y^{2}-50<0\):
Utilizando el corolario de la reducción por desigualdad podemos graficar unicamente la porción del lugar geométrico de \(F(x, y) = 0\) que se encuentra adentro de la circunferencia \(G(x,y)=0\), para ello definimos la ecuación implícita de reducción
\[F'(x, y) = F(x, y) \cdot \Phi(x, y) = F(x, y) \cdot \frac{\sqrt{-G(x,y)}}{\sqrt{-G(x,y)}} = 0\]reemplazando obtenemos
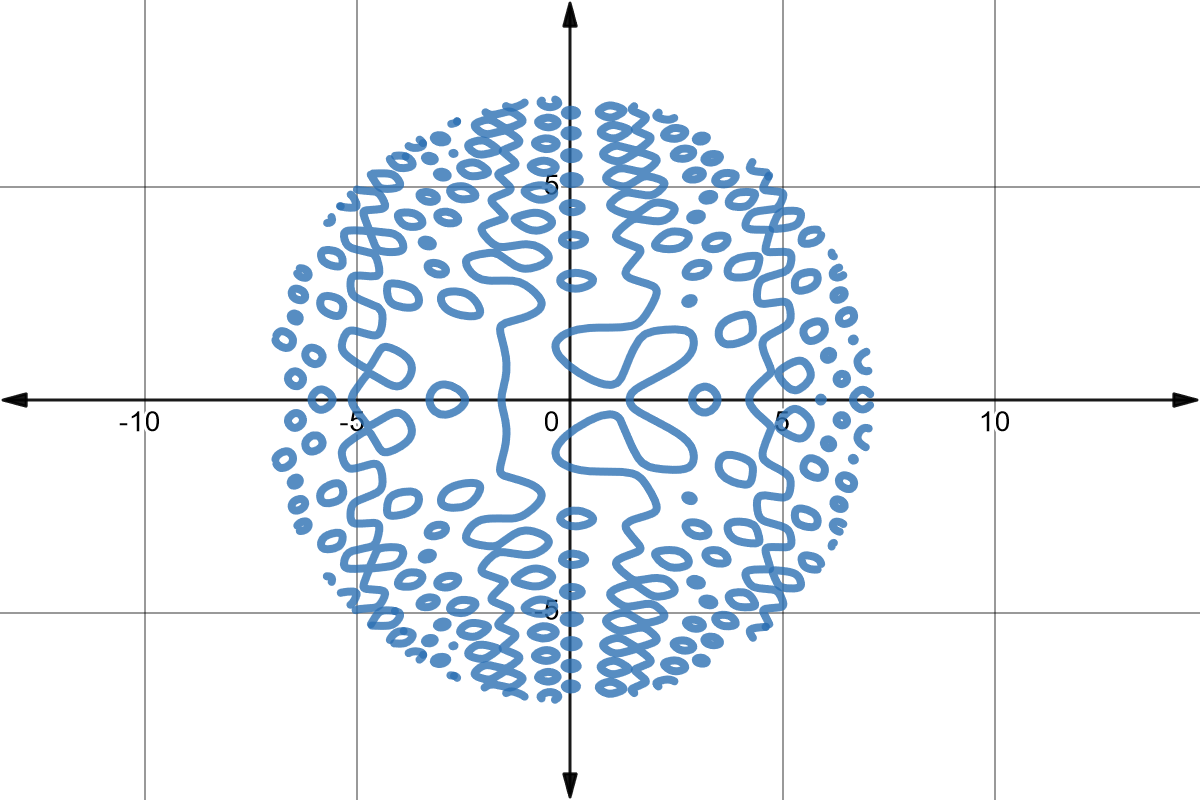
\[F'(x, y) = \cos\left(x+\cos\left(yx\right)-\sin\left(x^{2}-y^{2}\right)\right) \cdot \frac{\sqrt{50-x^{2}-y^{2}}}{\sqrt{50-x^{2}-y^{2}}} = 0\]Podemos visualizar la fascinante gráfica generada por \(F'(x, y) = 0\):
Construyendo una gráfica sorprendente
Después de analizar las propiedades de las ecuaciones implícitas y aprender cómo jugar con los lugares geométricos, tenemos a nuestra disposición un amplio conjunto de herramientas para construir una gráfica sorprendente.
Estrategia propuesta
En el proceso de construir una gráfica, es importante seguir una estrategia sólida que nos permita aprovechar las propiedades de las ecuaciones implícitas de manera efectiva. A continuación, proponemos una serie de pasos para crear tu propia gráfica sorprendente:
Definir el fondo de la gráfica: El primer paso es elegir una ecuación implícita \(F(x, y) = 0\) cuyo lugar geométrico funcionará como fondo de la gráfica. Esta ecuación implícita debe representar una forma interesante o un patrón que deseamos destacar en nuestra gráfica.
Determinar la forma deseada: A continuación, debemos definir la forma que tomará nuestra gráfica. Esto implica definir una ecuación implícita \(G(x, y)=0\) que contenga curvas interesantes, como círculos, elipses, hipérbolas, u otras curvas más complejas.
Explorar y ajustar: Es importante explorar diferentes opciones y ajustar los parámetros de las ecuaciones implícitas para obtener la gráfica deseada. Podemos experimentar con traslaciones, expansiones, compresiones, reflexiones y uniones para lograr efectos visuales interesantes.
Combinar las ecuaciones implícitas: Una vez que tengamos la ecuación implícita \(F(x, y) = 0\) como fondo de la gráfica y la ecuación implícita \(G(x, y) = 0\) como la forma deseada, combinaremos ambas ecuaciones mediante una reducción de lugares geométricos. Esto generará una ecuación implícita final \(M(x, y) = 0\) que representará nuestro resultado fin
Al seguir esta estrategia propuesta, podremos construir una gráfica sorprendente al combinar el fondo de la gráfica con una forma deseada utilizando la técnica de reducción de lugares geométricos. La creatividad y la experimentación jugarán un papel clave en este proceso, así que no dudes en probar diferentes ideas y ajustes para lograr el resultado deseado. A continuación encontrarás el proceso de construcción de la gráfica fascinante expuesta en la introducción.
Definiendo el fondo de la gráfica
Para el fondo de nuestra gráfica utilizaremos la ecuación implícita introducida en el ejemplo del corolario de la reducción por desigualdad.
\[F(x, y) = \cos\left(x+\cos\left(yx\right)-\sin\left(x^{2}-y^{2}\right)\right)=0\]Cuyo lugar geométrico es:
Determinando la forma de la gráfica
Para lograr la impresionante figura que presenta nuestra gráfica final, definiremos un número de ecuaciones implícitas \(G_i(x, y)=0\), donde cada una de estas representará una curva interesante que se combinará con las demás para formar la gráfica final \(G(x, y)=0\), aplicando la propiedad de unión de lugares geométricos:
\[G(x, y) = \prod_{i=1}^{n} G_i(x, y) = 0\]Comencemos por definir la ecuación implícita \(G_1(x, y)=0\), que representa una circunferencia de radio \(\sqrt{50}\) centrado en el origen:
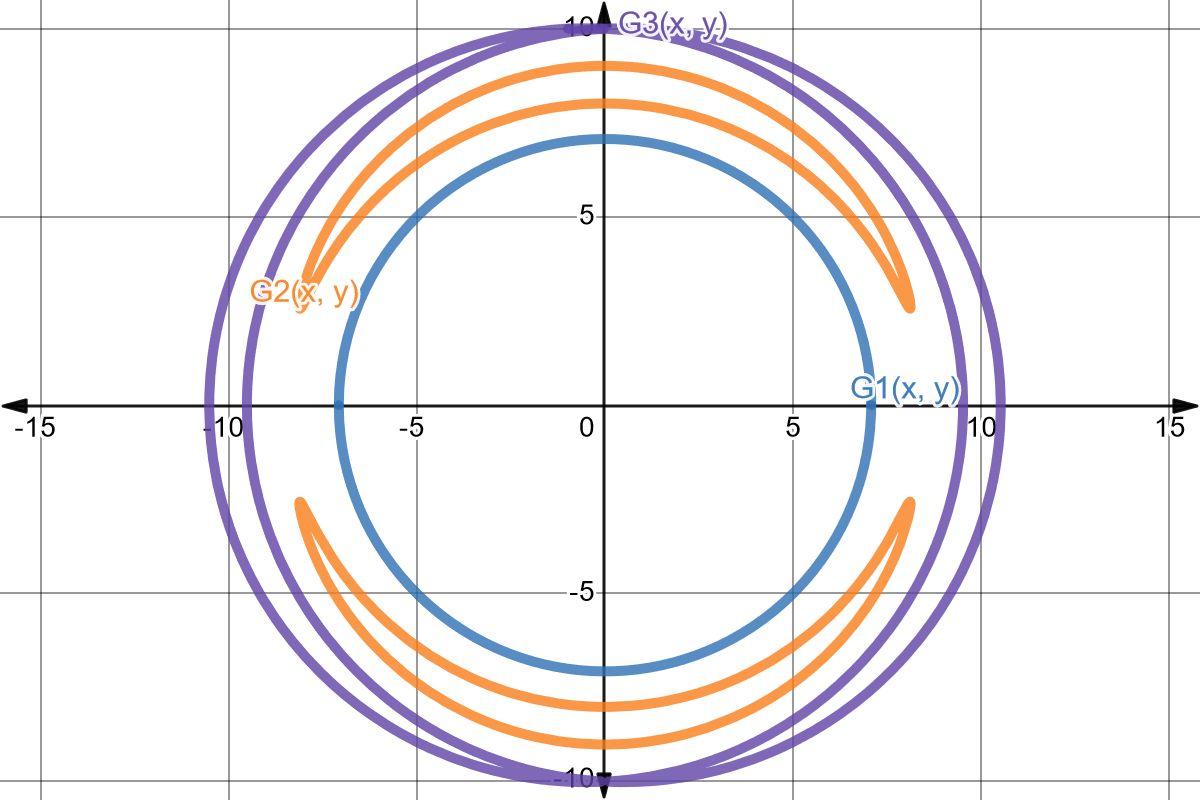
\[G_1(x,y)=x^{2}+y^{2}-50=0\]Luego establecemos la expresión \(G_2(x, y)=0\), cuyo lugar geométrico tiene la forma de dos lunas enfrentadas, donde el eje de simetría es \(y=0\):
\[G_2(x,y)=(y^{2}+x^{2}-8.5^{2})^{2}-(y^{2}-0.1x^{2})=0\]Finalmente, definimos la ecuación implícita \(G_3(x, y)=0\), la cual genera una curva con forma de dos lunas enfrentadas, tal como \(G_2(x, y)=0\), pero con eje de simetría \(x=0\):
\[G_3(x,y)=(x^{2}+y^{2}-10^{2})^{2}-x^{2}=0\]A continuación se muestra la gráfica de cada una de estas ecuaciones implícitas:
Así, la función \(G(x, y)\) que representa la forma deseada de nuestra gráfica es:
\[\begin{align*} G(x,y)&=G_1(x,y) \cdot G_2(x,y) \cdot G_3(x,y) \\ &=\left(x^{2}+y^{2}-50\right)\left((y^{2}+x^{2}-8.5^{2})^{2}-(y^{2}-0.1x^{2})\right)\left((x^{2}+y^{2}-10^{2})^{2}-x^{2}\right) \end{align*}\]Combinando las ecuaciones implícitas
Una vez conseguimos el fondo de la gráfica y la forma deseada, podemos combinar ambas ecuaciones implícitas mediante una reducción de lugares geométricos para obtener la gráfica final \(M(x, y) = 0\): Para combinar las ecuaciones implícitas \(F(x, y) = 0\) y \(G(x, y) = 0\), aplicamos la propiedad de unión de lugares geométricos:
\[M(x, y) = F(x, y) \cdot \frac{\sqrt{-G(x, y)}}{\sqrt{-G(x, y)}} = 0\]Reemplazando obtenemos la inmensa ecuación implícita:
\[M(x, y) = \cos\left(x+\cos\left(yx\right)-\sin\left(0.5x^{2}-y^{2}\right)\right)\ \frac{\sqrt{-\left(x^{2}+y^{2}-50\right)\left((y^{2}+x^{2}-8.5^{2})^{2}-(y^{2}-0.1x^{2})\right)\left((x^{2}+y^{2}-10^{2})^{2}-x^{2}\right)}}{\sqrt{-\left(x^{2}+y^{2}-50\right)\left((y^{2}+x^{2}-8.5^{2})^{2}-(y^{2}-0.1x^{2})\right)\left((x^{2}+y^{2}-10^{2})^{2}-x^{2}\right)}}=0\]cuyo lugar geométrico es:
Conclusión
En este blog, hemos explorado el fascinante mundo de las ecuaciones implícitas y cómo se pueden utilizar para crear gráficas sorprendentes. Hemos aprendido que una ecuación implícita es una relación de la forma \(F(x_1, \dots, x_n) = 0\), cuyo lugar geométrico es la gráfica de la misma. También hemos visto que una función implícita es una función definida mediante una ecuación implícita y que se relaciona una variable dependiente con las variables independientes.
A lo largo del blog, hemos analizado diversas propiedades de las ecuaciones implícitas que nos permiten trasladar, expandir, comprimir, reflejar y combinar lugares geométricos, lo cual nos brinda una amplia gama de posibilidades para crear gráficas sorprendentes. Además, hemos visto cómo podemos reducir los lugares geométricos mediante la eliminación de puntos específicos, utilizando técnicas como la reducción por distinción y la reducción por desigualdad.
Siguiendo una estrategia sólida, hemos propuesto una serie de pasos para construir nuestra propia gráfica sorprendente. Estos pasos incluyen la definición del fondo de la gráfica, la determinación de la forma deseada, la exploración y ajuste de parámetros, y la combinación de ecuaciones implícitas mediante reducciones de lugares geométricos.
Finalmente, hemos aplicado esta estrategia para construir una gráfica fascinante, combinando una ecuación implícita de fondo con varias ecuaciones implícitas que representan formas interesantes. Mediante la experimentación y ajuste de parámetros, hemos logrado crear una gráfica sorprendente que destaca por su belleza y complejidad.
En conclusión, hemos demostrado que se puede aprender mucho acerca de las ecuaciones implícitas jugando con las mismas, y que la creatividad y la experimentación son clave para descubrir nuevas formas de generar gráficas sorprendente. Así que ¡sigue explorando y divirtiéndote con las matemáticas!
Bibliografía
Lecture 24: Implicit Functions, Dartmouth College.
Álgebra y Geometría analítica, Universidad Tecnológica Nacional, Facultad Regional Buenos Aires.
Geometría III: Geometría analítica plana y del espacio, Elizabeth Vargas y Luis Núñez.